Задача 58127 [red]Пожалуйста, помогите! [/red] 1)...
Условие
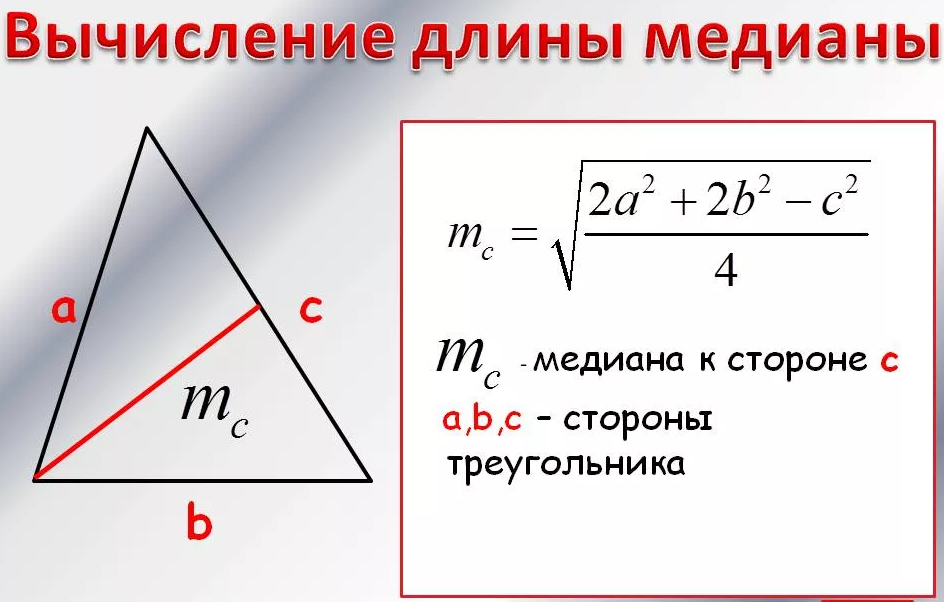
1) Две стороны треугольника равны 14см и 22см, длина медианы, проведенной к третьей стороне, 12см. Найти третью сторону треугольника.
2) Найдите радиус окружности, описанной около треугольника со сторонами 51см, 52см и 53см.
нет в списке 8-9 класс
1539
Решение
★
См скрин.
[m]12=\sqrt{\frac{2\cdot 14^2+2\cdot 22^2-x^2}{4}}[/m] ⇒
[m]x^2=2\cdot 196+2\cdot 484-144\cdot 4[/m]
[m]x^2=784[/m]
[m]x=28[/m]
2.
[m]S=\sqrt{p(p-a)(p-b)(p-c)}[/m]
[m]p=\frac{51+52+53}{2}=78[/m]
[m]S=\sqrt{78\cdot(78-51)\cdot(78-52)\cdot (78-53)}=\sqrt{3\cdot 26\cdot 27 \cdot 26\cdot 25}=26\cdot 9\cdot 5[/m]
[m]R=\frac{abc}{4S}=\frac{51\cdot 52\cdot 53}{4\cdot 26\cdot 9\cdot 5}=\frac{901}{30}[/m]