Задача 58108 ...

602ea5793cfdeb46290ca5ae

25.02.2021 19:26:23

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB = 4, BC = 3, AA₁ = 2. Точки P и Q — середины рёбер A₁B₁ и CC₁ соответственно. Плоскость APQ пересекает ребро B₁C₁ в точке U.

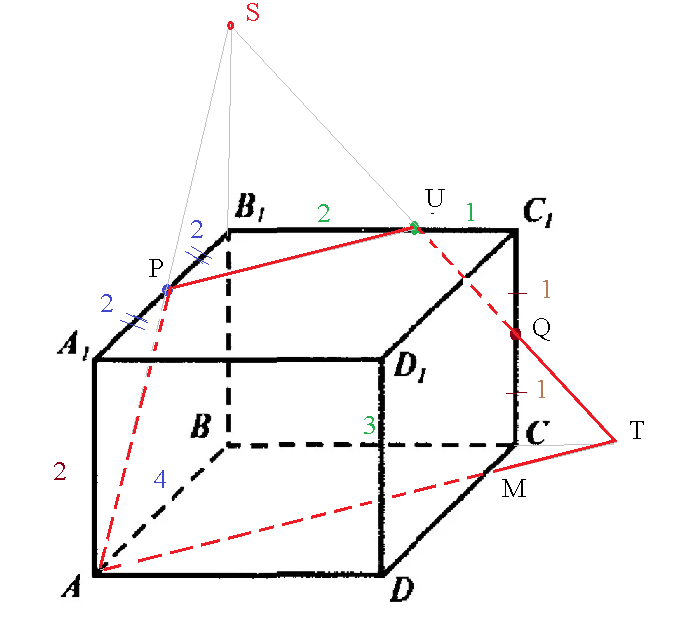
a) Докажите, что B₁U : UC₁ = 2 : 1.
б) Найдите площадь сечения параллелепипеда ABCDA₁B₁C₁D₁ плоскостью APQ.

5f3ea7e3faf909182968ddd9

25.02.2021 20:27:43

★

B_(1)C_(1)=3
B_(1)U:UC_(1)=2:1 ⇒

B_(1)U=[b]2[/b]
UC_(1)=[b]1[/b]

Δ PB_(1)U- прямоугольный равнобедренный PB_(1)=B_(1)U=[b]2[/b]
PU=[b]2sqrt(2)[/b]

Δ UC_(1)Q= ΔTCQ по катету и острому углу ⇒ UC_(1)=СТ=[b]1[/b]
AT=4sqrt(2)


Можно доказать из подобия, что
Δ SPU- равносторонний.

S_(Δ SPU )=(1/2)*2sqrt(2)*2sqrt(2)*sin60 °=2sqrt(3)

Δ SAT - равносторонний.

S_(Δ SAT )=(1/2)*4sqrt(2)*4sqrt(2)*sin60 °=8sqrt(3)

S_(трапеции APUT)=8sqrt(3)-2sqrt(3)=6 sqrt(3)

S_( Δ MQT)=(1/2)*sqrt(2)*sqrt(2)*sin60 °=sqrt(3)/2

S_([b]сечения[/b])=S_(трапеции APUT)-S_( Δ MQT)=6sqrt(3)-(sqrt(3)/2)=[b]11sqrt(3)/2[/b]