Задача 58086 ...

6020f0c7e2ae7f609a56a749

24.02.2021 13:46:29

3. Вычислите площадь криволинейной трапеции, ограниченной линиями: y = -x² + 2, y = 0, x = -3, x = 1.

5f3ea7e3faf909182968ddd9

24.02.2021 13:55:15

★

[m]S=S_{1}+S_{2}= ∫ ^{-\sqrt{2}}_{-3}(0-(-x^2+2))dx+∫^{1} _{-\sqrt{2}}((-x^2+2)-0)dx=[/m]


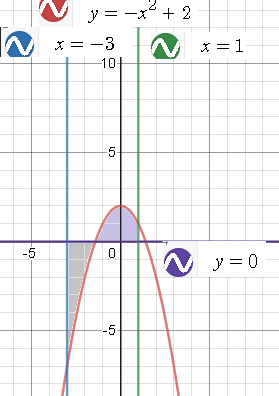
[m]=∫ ^{-\sqrt{2}}_{-3}(x^2-2)dx+∫^{1} _{-\sqrt{2}}(-x^2+2)dx=[/m]

[m]=(\frac{x^3}{3}-2x)|^{-\sqrt{2}}_{-3}+(-\frac{x^3}{3}+2x)|^{1} _{-\sqrt{2}}=...[/m]


-----------