Задача 58022 В треугольнике ABC стороны...

60314d323cfdeb46290cb25e

20.02.2021 20:56:29

В треугольнике ABC стороны AB:BC:AC=3:4:5. Первая окружность вписана в треугольник АВС, а вторая касается AB и продолжения сторон BC и AC.

А) Доказать, что отношение радиусов окружностей равно 1:2.
Б) Найти расстояние между точками касания окружностей стороны AB, если АС=15.

5f3ea7e3faf909182968ddd9

21.02.2021 00:06:54

★

AB:BC:AC=3:4:5 ⇒ AB=3k;BC=4k; AC=5k

Δ АВС - прямоугольный, так как

АС^2=AB^2+BC^2

(5k)^2=(3k)^2+(4k)^2

r_(окр вписанной в Δ АВС)=k

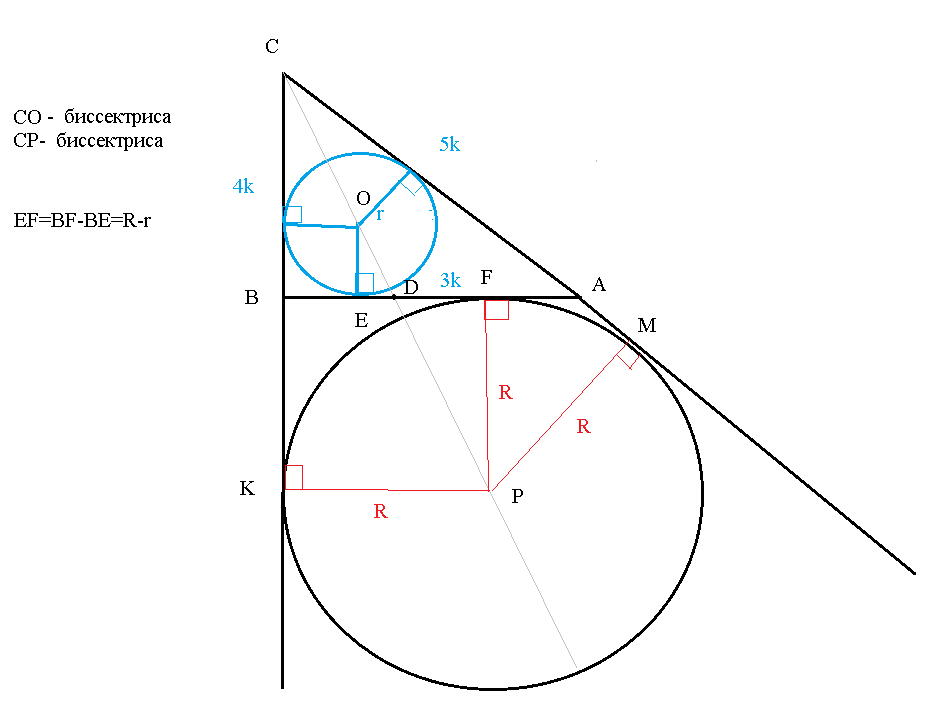
Cм. скрин
Центр окружности, вписанной в треугольник АВС - точка пересечения биссектрис.

Значит CO- биссектриса угла С

Вторая окружность вписана в угол ВСА.

Центр этой окружности лежит на биссектрисе угла С

СP- биссектриса.

Значит, точки С,О,Р - лежат на одной прямой

Далее подобие.


(4k-r):(4k+R)=r:R ⇒

3k:(4k+R)=k:R

3kR=4k^2+KR

2kR=2k^2

R=2k

r:R=k:2k=[b]1:2[/b]

б)
АС=15

5k=15

k=3

r=3
R=6

EF=6-3=[b]3[/b]