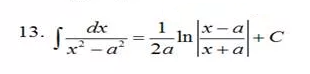Задача 57944 ...
Условие
Решение
Разложить дробь на простейшие.
D > 0
[m]3x^2-8x-3=(3x+1)(x-3)[/m]
[m]\frac{1}{3x^2-8x-3}=\frac{A}{3x+1}+\frac{B}{x-3}[/m]
[m]\frac{1}{3x^2-8x-3}=\frac{A(x-3)+B(3x+1)}{(3x+1)(x-3)}[/m]
[m]1=A(x-3)+B(3x+1)[/m] ⇒
[m]\left\{\begin {matrix}0=A+3B\\1=-3A+B\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}A=-3B\\1=-3\cdot (-3B)+B\end {matrix}\right.[/m]⇒ [m]\left\{\begin {matrix}A=-0,3\\B=0,1\end {matrix}\right.[/m]
[m] ∫ \frac{1}{3x^2-8x-3}dx=-0,3 ∫ \frac{1}{3x+1}dx+0,1 ∫ \frac{1}{x-3}dx=[/m]
[m]=-0,3\cdot \frac{1}{3}∫ \frac{d(3x+1)}{3x+1}+0,1 ∫ \frac{d(x-3)}{x-3}=-0,1ln|3x+1|+0,1ln|x-3|+C=0,1ln|\frac{x-3}{3x+1}|+C[/m]
2 способ
Выделить полный квадрат
[m]3x^2-8x-3=3\cdot (x^2-\frac{8}{3}-1)=3\cdot(x^2-2\cdot x\cdot \frac{8}{6}+( \frac{8}{6})^2-( \frac{8}{6})^2-1)=[/m]
[m]=3\cdot ((x-\frac{8}{6})^2-( \frac{10}{6})^2)=3\cdot ((x-\frac{4}{3})^2-( \frac{5}{3})^2)[/m]
[m] ∫ \frac{1}{3x^2-8x-3}dx=∫ \frac{1}{3\cdot ((x-\frac{4}{3})^2-( \frac{5}{3})^2)}dx=\frac{1}{3}∫ \frac{d(x-\frac{4}{3})}{(x-\frac{4}{3})^2-( \frac{5}{3})^2}=\frac{1}{3}\cdot \frac{1}{2\cdot \frac{5}{3}}ln|\frac{x-\frac{4}{3}-\frac{5}{3}}{x-\frac{4}{3}+\frac{5}{3}}|+C=0,1ln|\frac{x-3}{x+\frac{1}{3}}|+C[/m]
Применили формулу: