Задача 57800 Найти площадь фигуры, ограниченной...
Условие
математика колледж
1293
Решение
★
[m]=\frac{x^3}{3}-4\frac{x^2}{2}+4x)| ^{2}_{0}=\frac{8}{3}-8+8=\frac{8}{3}[/m]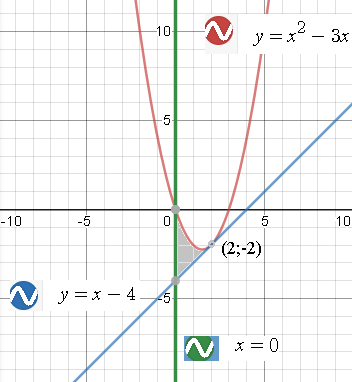
[m]=\frac{x^3}{3}-4\frac{x^2}{2}+4x)| ^{2}_{0}=\frac{8}{3}-8+8=\frac{8}{3}[/m]