Задача 57725 ...
Условие
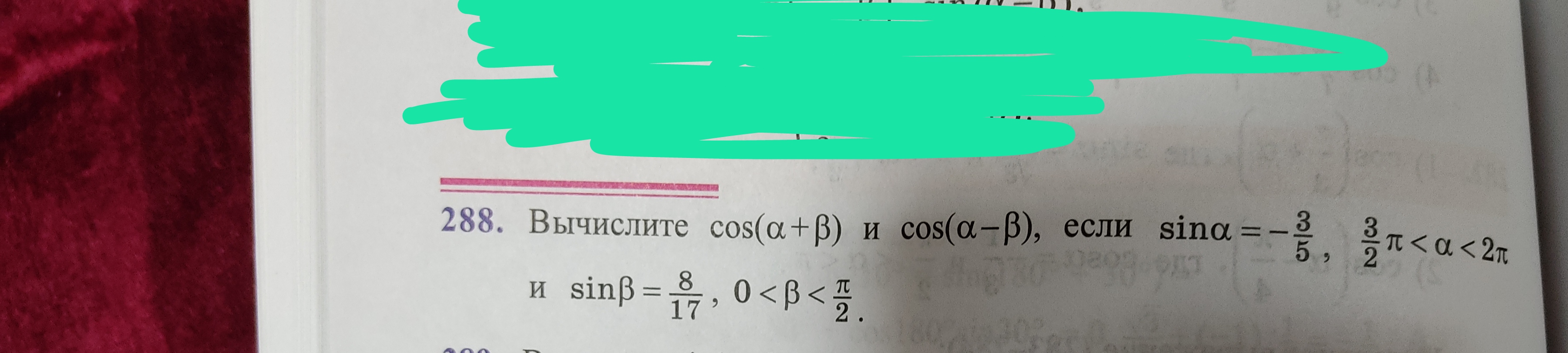
Решение
[m]cos(\alpha+\beta)=cos \alpha\cdot cos\beta-sin\alpha\cdot sin\ beta[/m]
Так как [m] sin^2\alpha+cos^2\alpha=1[/m] ⇒ [m]cos^2\alpha=1- sin^2\alpha=1-(-\frac{3}{5})^2=\frac{16}{25}[/m]
[m]cos\alpha=\pm\frac{4}{5}[/m] и так как [red][m]\frac{3\pi}{2}<\alpha <2\pi[/m][/red], это четвертая четверть,
косинус имеет знак +,
получаем:
[m]cos\alpha=+\frac{4}{5}[/m]
Аналогично
Так как [m] sin^2\beta+cos^2\beta=1[/m] ⇒ [m]сos^2\beta=1- sin^2\beta=1-(\frac{8}{17})^2=\frac{225}{289}[/m]
[m]sin\beta=\pm\frac{15}{17}[/m] и так как [green][m]0<\beta<\frac{\pi}{2} [/m][/green], это первая четверть,
косинус имеет знак +
получаем :
[m]cos\beta=+ \frac{15}{17}[/m]
Подставляем найденные значения в формулу и получаем ответ:
[m]cos(\alpha+\beta)=\frac{4}{5}\cdot\frac{15}{17}-(-\frac{3}{5})\cdot\frac{8}{17}=\frac{60}{85}+\frac{24}{85}=\frac{84}{85}=[/m]
О т в е т. [m]cos(\alpha+\beta)=\frac{84}{85}[/m]