Задача 57724 ...
Условие
2) sin(π/4 - α), где sinα = √2/3 и π/2 < α < π.
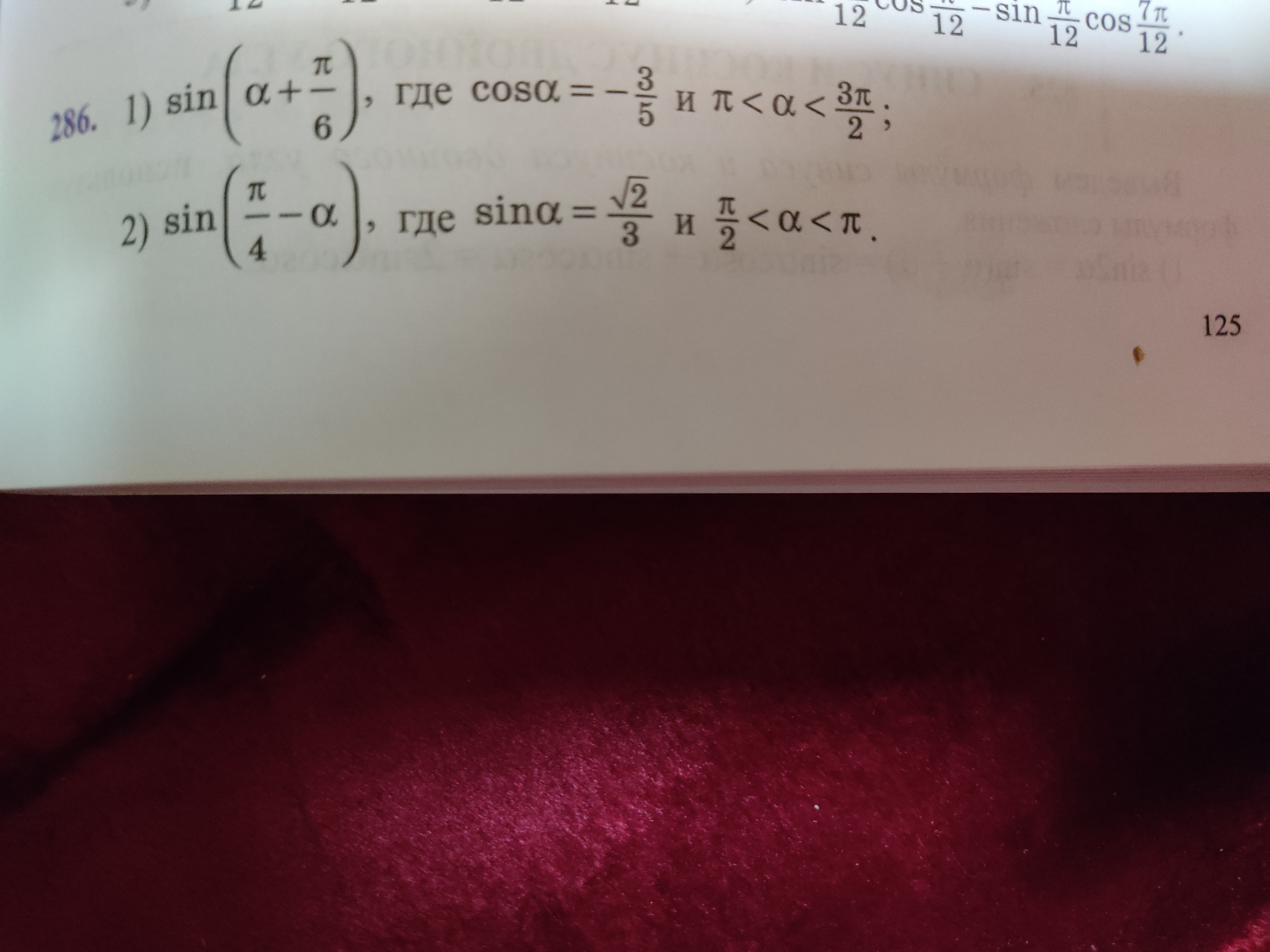
математика 8-9 класс
690
Решение
★
[m]sin(\alpha+\frac{\pi}{6})=sin \alpha\cdot cos\frac{\pi}{6}+cos\alpha\cdot sin\frac{\pi}{6}[/m]
Так как [m] sin^2\alpha+cos^2\alpha=1[/m] ⇒ [m]sin^2\alpha=1- cos^2\alpha=1-(-\frac{3}{5})^2=1-\frac{9}{25}=\frac{16}{25}[/m]
[m]sin\alpha=\pm\frac{4}{5}[/m] и так как [red][m]\pi <\alpha<\frac{3 \pi}{2}[/m][/red], это третья четверть,
синус имеет знак -,
получаем:
[m]sin\alpha=-\frac{4}{5}[/m]
[m]sin(\alpha+\beta)=(-\frac{4}{5})\cdot(\frac{\sqrt{3}}{2})+(-\frac{3}{5})\cdot \frac{1}{2}=\frac{-4\sqrt{3}-3}{10}[/m]
О т в е т. [m]sin(\alpha+\frac{\pi}{6})=\frac{-4\sqrt{3}-3}{10}[/m]