Задача 57492 ...
Условие
cos β = -√2/2 , π/2 < β < π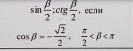
математика 10-11 класс
526
Решение
★
так как [m] \frac{π}{2}< β <π[/m] ⇒ [m] \frac{π}{4}< \frac{ β }{2} <\frac{π}{2}[/m] - первая четверть
синус и косинус имеют знак +
[m]sin\frac{ β }{2}=\frac{1}{2} [/m] ⇒ [m]cos\frac{ β }{2}=\frac{\sqrt{3}}{2} [/m]
[m] tg \frac{ β }{2}=\frac{sin\frac{ β }{2}}{cos\frac{ β }{2}}=\frac{1}{\sqrt{3}}[/m]