Задача 56692 ...

5fdf2a6fec9d2930a08993a9

02.01.2021 11:55:28

Найдите площадь внутри кривой r = 2cos(4φ), но вне круга r = 1.

5f3ea7e3faf909182968ddd9

02.01.2021 12:12:07

★

2cos(4φ) = 1 ⇒ cos4 φ =1/2 ⇒ 4 φ = ± (π/3)+2πn, n ∈[b] Z[/b]

φ =± (π/12)+(π/2)*n, n ∈[b] Z[/b]

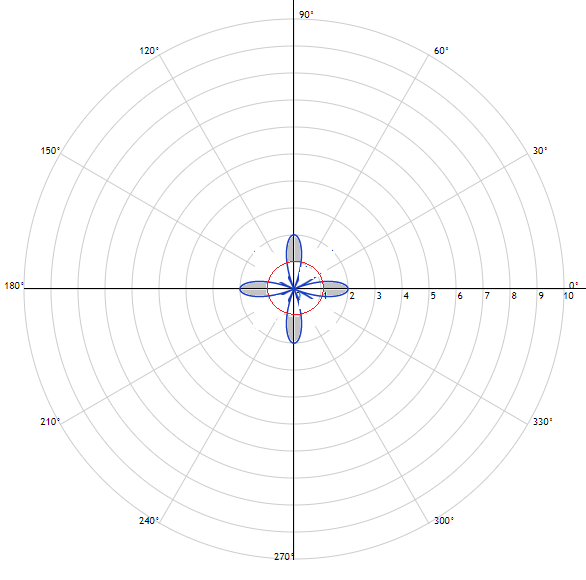
Найдем площадь одной части ( см. скрин 1) и умножим на 4

[m]S=4\cdot (S_{2}-S_{1})=4\cdot \frac{1}{2} ∫ ^{\frac{π}{12}}_{-\frac{π}{12}} (2cos4 φ)^2d φ -4\cdot \frac{1}{2} ∫ ^{\frac{π}{12}}_{-\frac{π}{12}}1^2d φ =[/m]

формула: [m]2cos^2 α =1+cos2 α [/m]

[m]=2\cdot ∫ ^{\frac{π}{12}}_{-\frac{π}{12}}4\cdot (1+cos8 φ )d φ -2\cdot ∫ ^{\frac{π}{12}}_{-\frac{π}{12}}d φ =(8 φ +sin8 φ-2 φ ) |^{\frac{π}{12}}_{-\frac{π}{12}}=(6φ +sin8 φ ) |^{\frac{π}{12}}_{-\frac{π}{12}}=π+2sin\frac{2π}{3}=π+1[/m]