Задача 56416 исследовать функцию и построить график...
Условие
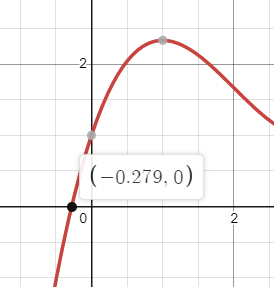
По графику функции определить число
её нулей. Используя метод деления отрезка пополам, найти нули
функции с точностью 0,1.
Решение
y`=x^2-4x+3
y`=0
x^2-4x+3=0
D=16-12=4
x_(1)=(4-2)/2=1; x_(2)=(4+2)/2=3
__+__ (1) __-___ (3) __+__
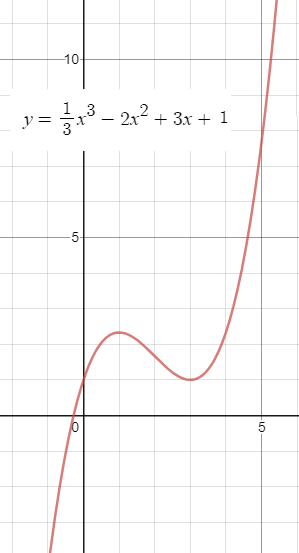
y`>0 на (- ∞ ;1) и на (3;+ ∞ ), значит функция возрастает
y`< 0 на (1 ;3), значит функция убывает
х=1 - точка максимума, производная меняет знак с + на -
у(1)=(1/3)*(1)^3-2*(1)^2+3*(1)+1=2 целых 1/3
х=3 - точка минимума, производная меняет знак с - на +
y(3)=(1/3)*(3)^3-2*(3)^2+3*(3)+1=1
y``=2x-4
y``=0
2x-4=0
x=2- точка перегиба, вторая производная меняет знак с - на +
Функция выпукла вверх на ( (- ∞ ;2) и выпукла вниз на (2;+ ∞ )
См. график рис. 1
Нахождение корней уравнения:
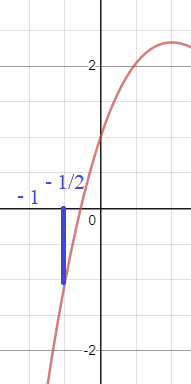
см. рис. 2
f(-1/2) <0
f(0) >0
⇒ корень на [-1/2; 0]
[red]Делим его пополам[/red]
Получаем два отрезка.
[-1/2;-1/4] и [-1/4;0]
Проверяем на концах какого отрезка функция принимает значения разных знаков
f(-1/4)=(1/3)*(-1/4)^3-2*(-1/4)^2+3*(-1/4)+1>0
Значит корень принадлежит отрезку [-1/2;-1/4]
[red]Делим его пополам.[/red]
Получаем два отрезка.
[-1/2;-3/8] и [-3/8;-1/4]
Проверяем на концах какого отрезка функция принимает значения разных знаков
f(-3/8)=(1/3)*(-3/8)^3-2*(-3/8)^2+3*(-3/8)+1<0
Значит корень принадлежит отрезку [-3/8;-1/4] ⇒ -0,375 < x < -0,25
[red]Делим его пополам.[/red]
...