Задача 56385 Решить задачу Коши.Помогите...
Условие
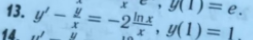
Решение
y`-(1/x)*y=-2(lnx)/x [red](#)[/red]
Решаем [i]однородное[/i]
y`-(1/x)*y=0
Это уравнение с [i]разделяющимися переменными[/i]:
dy/dx=y/x
dy/y=dx/x
∫ dy/y= ∫ dx/x
ln|y|=ln|x|+lnC
ln|y|=lnC*|x|
y=Cx
Применяем метод вариации произвольной С
y=C(x)*x
y`=C`(x)*x+C(x)*x`
y`=C`(x)*x+C(x)
Подставляем в [red](#)[/red]
C`(x)*x+C(x)-C(x)=-2(lnx)/x
C`(x)*x=-2(lnx)/x
C`(x)=-2(lnx)/x^2
C(x)= -2∫ (lnx/x^2)dx
применяем метод интегрирования по частям
[m]u=lnx[/m] ⇒ [m]du=dx/x[/m]
[m]dv=dx/x^2[/m] ⇒ v=(-1/x)
-2∫ (lnx/x^2)dx=-2*(lnx*(-1/x))+2 ∫(-1/x)dx=-2*(lnx*(-1/x)+C)-2 ∫(1/x)dx=2*(lnx*(-1/x)+C)-2 lnx + C
y=C(x)*x=(2*(lnx*(-1/x)+C)-2 lnx + C)*x
y=[b]-2lnx-2Cx*lnx+Cx[/b] - общее решение
При х=1 y=1
1=-2ln1 -2C*ln1+C*1 ⇒ C=1
y=[b]-2lnx-2x*lnx+x[/b] - решение, удовлетворяющее условию y(1)=1
