Задача 56344 2 сложных уравнения, подробно распишите...
Условие
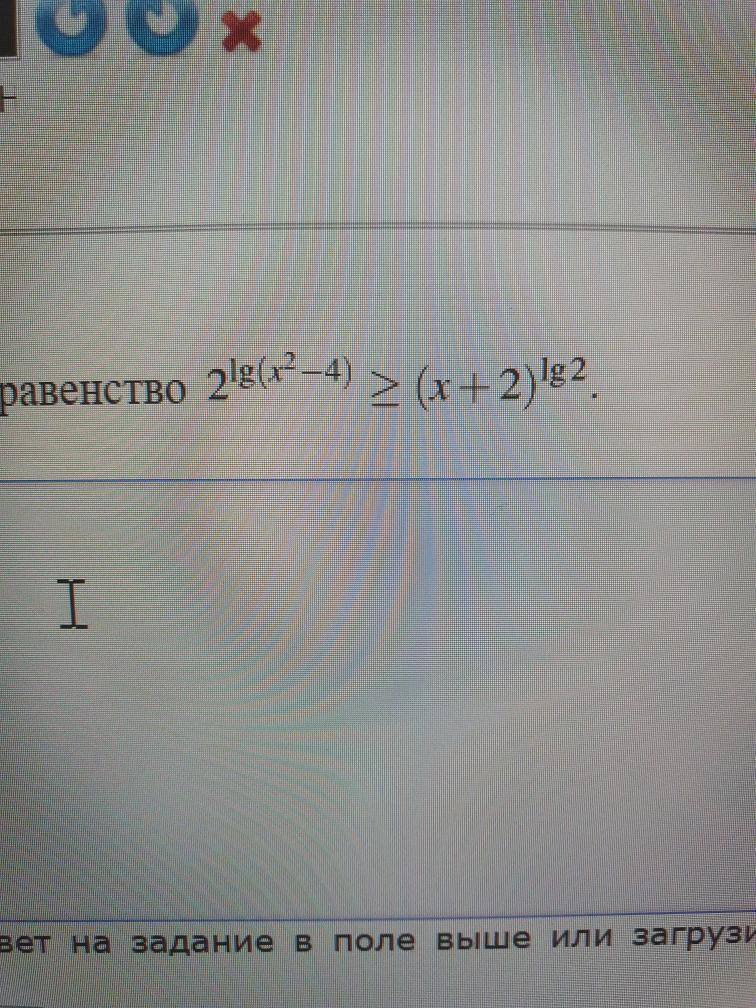

Решение
{x^2-4>0
{x+2>0
[red]x>2[/red]
Метод решения таких неравенств: логарифмирование обеих частей.
Так как основание логарифма 10 >1, логарифмическая функция [b]возрастает[/b], знак неравенства не меняется
[m]lg2^{lg(x^2-4)} ≥ lg(x+2)^{lg2}[/m]
Применяя [b]свойства логарифма степени[/b] получим:
[m]lg(x^2-4)\cdot lg2≥ lg2\cdot lg(x+2)[/m]
Делим на lg 2 и получаем несложное логарифмическое неравенство:
lg(x^2-4)≥lg(x+2)
По свойству возрастания логарифмической функции с основанием 10>1
x^2-4≥x+2
(x-2)*(x+2)-(x+2)≥0
(x+2)*(x-2-1)≥0
{x+2)*(x-3) ≥0
Применяем метод интервалов на ОДЗ
(2) __-___[3] ___+___
О т в е т. [3;+ ∞ )
2.
Замена переменной:
[m]2^{x}=t[/m], [red][b]t >0[/b][/red]
По свойствам степени:
[m]2^{-x}=\frac{1}{t}[/m]
[m]4^{-x}=\frac{1}{t^2}[/m]
[m]2^{5+x}=2^{5}\cdot 2^{x}=32t[/m];
[m]2^{3-x}=2^{3}\cdot 2^{-x}=8t[/m]
Получаем [b]дробно- рациональное неравенство[/b]:
[m]\frac{32\cdot t-\frac{1}{t}}{8\cdot \frac{1}{t}-\frac{1}{t^2}} ≥ t[/m] ⇒ [m]\frac{(32t^2-1)\cdot t}{8t-1} ≥ t[/m] ⇒ [m]\frac{(32t^2-1)\cdot t}{8t-1}-t ≥ 0[/m]
[m]t\cdot (\frac{32t^2-1}{8t-1}-1) ≥ 0[/m]
[red][b]t >0[/b][/red] ⇒ [m]\frac{32t^2-1}{8t-1}-1 ≥ 0 ⇒ \frac{32t^2-1-8t+1}{8t-1} ≥ 0 ⇒ \frac{8t\cdot (4t-1)}{8t-1} ≥ 0 [/m]
применяем метод интервалов на ОДЗ:
(0) ___+__ (1/8) ___-__ [1/4] __+___
0 < t < 1/8 или t ≥ 1/4
2^(x) <1/8 или 2^(x) ≥ 1/4
2^(x) <2^(-3) или 2^(x) ≥ 2^(2)
x <-3 или x ≥ 2
О т в е т. (- ∞ ;-3) U [2;+ ∞ )
Все решения


