Задача 56071 ...
Условие
9. y = 1 / x√(1 + ln x), y = 0, x = 1, x = e^3.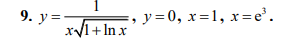
математика колледж
481
Решение
★
Применяем формулу Ньютона Лейбница и получаем ответ.
Применили формулу
[m] ∫ \frac{du}{\sqrt{u}}=2\sqrt{u}+C[/m]
u=1+lnx
du=(1/x)dx
