Задача 55643 площадь фигуры ограниченной линиями...
Условие
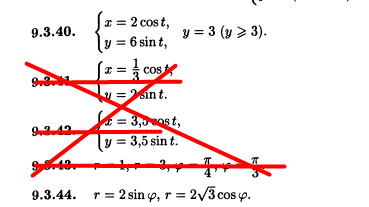
математика ВУЗ
1158
Решение
★
[m]\frac{x}{2}=cost[/m]
[m]\frac{y}{6}=sint[/m]
Возводим в квадрат и складываем:
[m]\frac{x^2}{4}+\frac{y^2}{6}=1[/m]
Это эллипс.
Площадь фигуры находим по формуле, площадь под кривой, заданной параметрически. См. скрин
44.
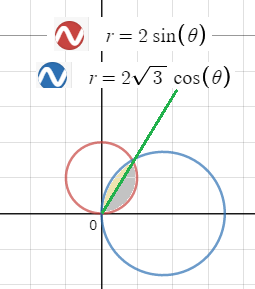
2sin φ =2sqrt(3)cos φ ⇒ tg φ =sqrt(3); φ =π/3
[m]S=S_{1}+S_{2}= ∫^{\frac{π}{3}} _{0}(2sin φ )d φ +∫^{\frac{π}{2}} _{\frac{π}{3}}(2\sqrt{3}cos φ )d φ=[/m]
[m]=2\cdot (-cos φ )|^{\frac{π}{3}} _{0}+2\sqrt{3}(sin φ )|^{\frac{π}{2}} _{\frac{π}{3}}=...[/m]