Задача 555 а) Решите уравнение...
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку [-2Pi/-Pi/2]
математика 10-11 класс
69481
Решение
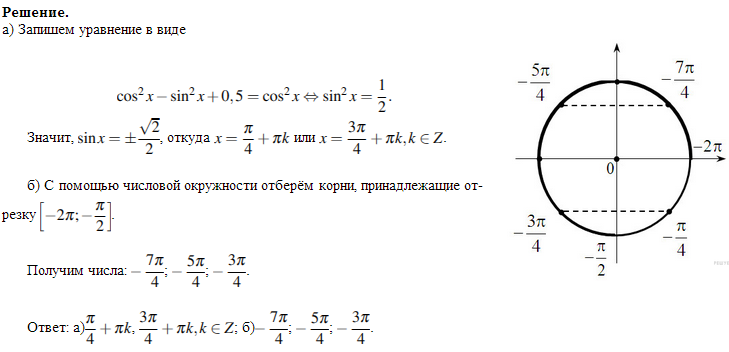
Ответ: в решение
