Задача 55423 Исследовать методами дифференциального...

5fa6de8d6c239d30d9b66c52

07.11.2020 20:51:31

Исследовать методами дифференциального исчисления функцию и построить её график

5f3ea7e3faf909182968ddd9

07.11.2020 21:35:01

★

Область определения (– ∞;3)U(3;+ ∞ )

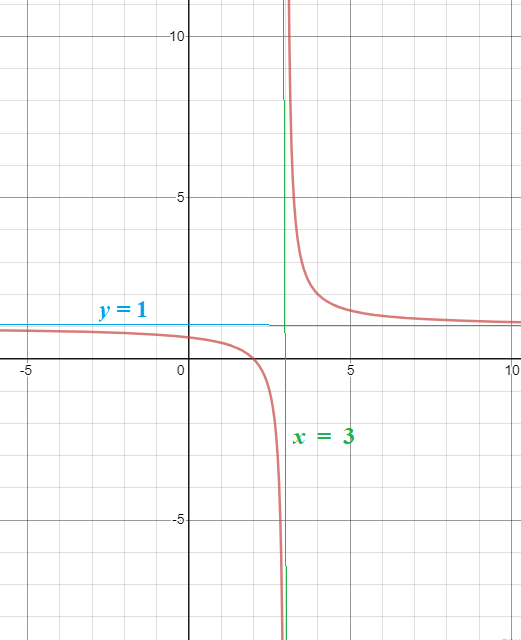
Прямая x=3 - вертикальная асимптота, так как lim_(x → 3)f(x)= ∞

Прямая y=1 - горизонтальная асимптота, так как lim_(x → ∞ )f(x)= 1


Функция не является ни чётной, ни нечётной

y(-x)=(2-(-x))/(3-(-x))=(2+x)/(3+x)

y(-x) ≠ y(x) и y(-x) ≠ -y(x)


Находим производную:

y`=((2-x)`·(3–x)–(2-x)·(3–x)`)/(3–x)^2

y`=((-1)·(3–x)–(2-x)·(–1))/(3–x)^2

y`=(-1)/(3–x)^2

y` < 0 на (– ∞;3) и на (3;+ ∞ )

Функция убывает на (– ∞;3) и на (3;+ ∞ )

График см. рис.