Задача 55366 ...
Условие
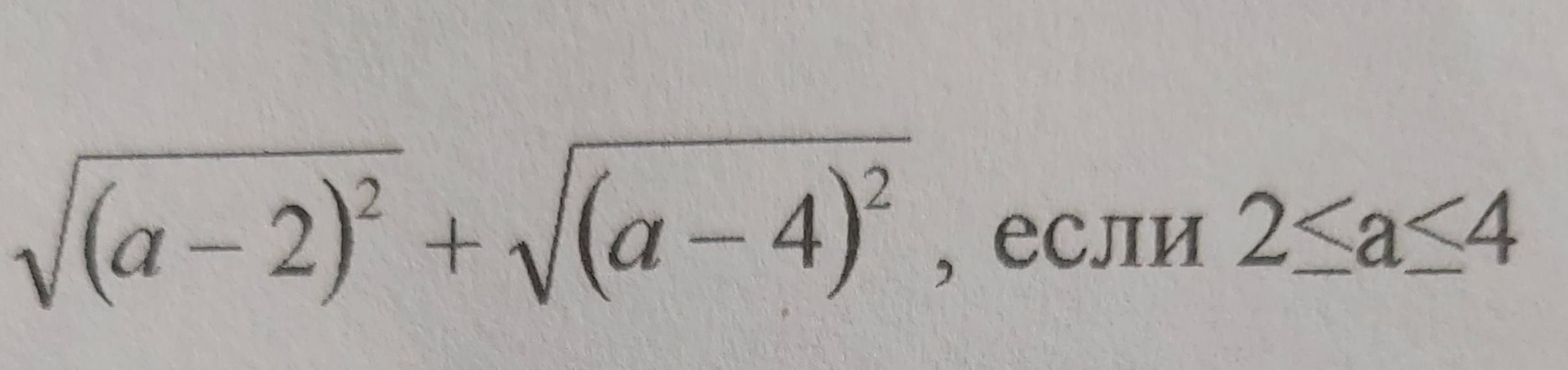
математика 10-11 класс
613
Решение
★
[m]\sqrt{(a-2)^2}=|a-2|[/m],
[m]\sqrt{(a-4)^2}=|a-4|[/m].
[m]|x|=\left\{\begin{matrix}
x, если x ≥ 0 \\ -x , если x < 0\end{matrix}\right.[/m]
[m]|a-2|=a-2[/m], так как [m]2 ≤ a ≤ 4[/m]и значит [m] a-2 ≥ 0[/m],
модуль неотрицательного выражения есть само это выражение
[m]|a-4|=-(a-4)[/m], так как [m] a ≤ 4[/m] и значит [m] a-4 ≤ 0[/m],
модуль отрицательного выражения есть выражение ему противоположное.
[m]\sqrt{(a-2)^2}+\sqrt{(a-4)^2}=|a-2|+|a-4|=a-2+(-(a-4))=a-2-a+4=2[/m]
Ответ: 2
Все решения
sqrt(a-2)^2)+sqrt((a-4)^2)=|a-2|+|a-4|=a-2+4-a=2 ( так как по условию
2 ≤ a ≤ 4 , то (a-2)>0, (a-4)<0)
Ответ: 2