Задача 55363 Вычислить объем тела, полученного от...
Условие
математика колледж
823
Решение
★
[m]=π(\frac{4^5}{5}-8\frac{4^4}{4}+16\frac{4^3}{3})=...[/m]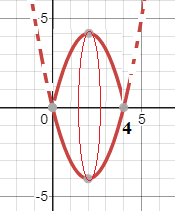
[m]=π(\frac{4^5}{5}-8\frac{4^4}{4}+16\frac{4^3}{3})=...[/m]