Задача 55252 Срочно! Проверить равенство! ...
Условие
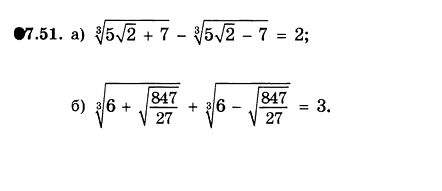
математика 10-11 класс
881
Решение
★
Возводим в куб по формуле: [m](\sqrt[3]{x}-\sqrt[3]{y})^3=(\sqrt[3]{x})^3-3(\sqrt[3]{x})^2\cdot (\sqrt[3]{y})+3(\sqrt[3]{x})\cdot (\sqrt[3]{y})^2-(\sqrt[3]{y})^3[/m]
получаем:
[m](5\sqrt{2}+7 )-3\sqrt[3]{5\sqrt{2}+7)^2\cdot (5\sqrt{2}-7)}+3\sqrt{(5\sqrt{2}+7)(5\sqrt{2}-7)^2}-(5\sqrt{2}-7)=2^3[/m]
[m]5\sqrt{2}+7 -3\sqrt[3]{(5\sqrt{2}+7)\cdot (5\sqrt{2}-7)}\cdot (\sqrt{5\sqrt{2}+7}-\sqrt{5\sqrt{2}-7})-5\sqrt{2}+7=2^3[/m]
[m]7 -3\sqrt[3]{(5\sqrt{2})^2-7^2}\cdot 2+7=2^3[/m]
[m]7 -3\sqrt[3]{50- 49}\cdot 2+7=2^3[/m]
[m]7 -6+7=2^3[/m]
[m]8=8[/m] - верно