Задача 55250 ...
Условие
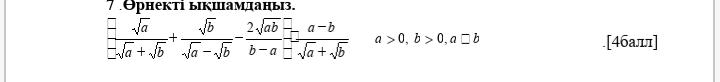
Решение
[m]a-b=(\sqrt{a})^2-(\sqrt{b})^2=(\sqrt{a}-\sqrt{b})\cdot (\sqrt{a}+\sqrt{b})[/m]
[m]\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}+\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\frac{2\sqrt{ab}}{a-b}=\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}+\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\frac{2\sqrt{ab}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{\sqrt{a}\cdot (\sqrt{a}-\sqrt{b})+\sqrt{b}\cdot (\sqrt{a}+\sqrt{b})+2\sqrt{ab}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=[/m]
[m]=\frac{\sqrt{a}\cdot \sqrt{a}-\sqrt{a}\cdot\sqrt{b}+\sqrt{b}\cdot \sqrt{a}+\sqrt{b}\cdot \sqrt{b}+2 \sqrt{ab}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{(\sqrt{a})^2+(\sqrt{b})^2+2 \sqrt{ab}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{(\sqrt{a}+\sqrt{b})^2}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}[/m]