Задача 55243 решите уравнение ...
Условие
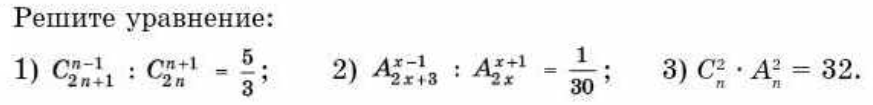
математика 10-11 класс
560
Решение
★
[m] С^{n+1}_{2n}=\frac{(2n)!}{(n+1)!\cdot (2n-(n+1)!}=\frac{(2n)!}{(n+1)!\cdot (n-1)!}[/m]
[m]\frac{ С^{n-1}_{2n+1}}{С^{n+1}_{2n}}=\frac{(2n+1)!}{(n-1)!\cdot (n+2)!} : \frac{(2n)!}{(n+1)!\cdot (n-1)!}=\frac{(2n+1)!}{(n-1)!\cdot (n+2)!} \cdot \frac{(n+1)!\cdot (n-1)!}{(2n)!}=\frac{(2n)!\cdot (2n+1)}{ (n+1)!\cdot (n+2)} \cdot \frac{(n+1)!}{(2n)!}=\frac{2n+1}{n+2}[/m]
Осталось решить уравнение:
[m]\frac{2n+1}{n+2}=\frac{5}{3}[/m]
n=7
Ответ: 7