Задача 55236 Исследовать функцию и построить...

лисёнок

1 ноября 2020 г. в 16:58

Исследовать функцию и построить график:
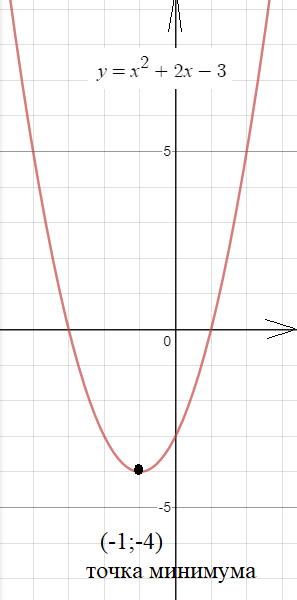
[m]y = x^2 + 2x - 3,[/m]
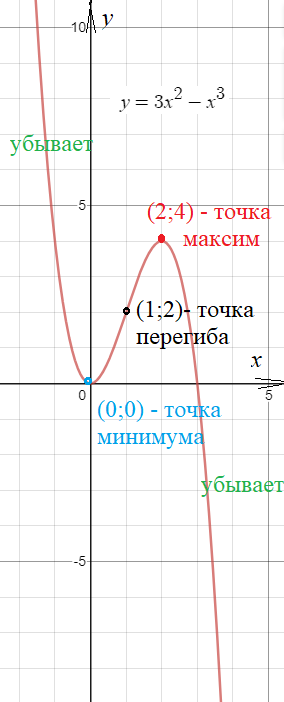
[m]f(x) = 3x^2 - x^3[/m]

exponenta

1 ноября 2020 г. в 18:13

★

1.
Область определения (– ∞ ;+ ∞ )

y`=(3x<sup>2</sup>–x<sup>3</sup>)`=6x–3x²
y`=0
6x–3x²=0
3x·(2–x)=0
x=0 или х=2

Расставляем знак производной

Например, так : y`(10) <0
далее чередуем справа налево:

__–__ (0) _+___ (2) ___–__

х=2 – точка максимума, производная меняет знак с + на –
х=0 – точка минимума, производная меняет знак с – на +

y`< 0 на (– ∞ ;0) и на (2;+ ∞ )
Функция убывает на на (– ∞ ;0) и на (2;+ ∞ )

y`>0 на (0;2)
Функция возрастает на на (0;2)


y``=(6x–3x²)`

y``=6–6x

y``=0

x=1 – точка перегиба, вторая производная меняет знак с + на –

y``>0 на (– ∞ ;1)
Функция выпукла вниз на (– ∞ ;1)

y``< 0 на (1;+ ∞ )
Функция выпукла вверх на (1;+ ∞ )



2.
Область определения (– ∞;+ ∞)

f`(x)=(x<sup>2</sup>+2x–3)`


f`(x)=2x+2

f`(x)=0

2x+2=0

х= –1

Знак производной

__–__ (–1) __+__

y`< 0 на (– ∞; –1)

значит функция убывает на (– ∞; –1)


y`>0 на (–1 ;+ ∞)

значит функция возрастает на (–1 ;+ ∞)




x=–1 – точка минимума, производная меняет знак с – на +


y``=(2x+2)`

y``=2 >0

y`` < 0 при х < 0


кривая выпукла вниз на (– ∞ ;+ ∞)

точек перегиба нет