Задача 55229 Вычислить пределы функций, не используя...
Условие
(вариант на фото)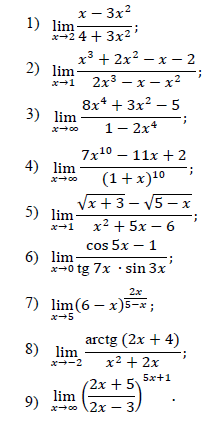
Решение
[m]=\lim_{x \to 2 }\frac{x-3x^2}{4+x^2}=\frac{2-3\cdot 2^2}{4+2^2}=-\frac{5}{4}[/m]
2
[m]\lim_{x \to 1 }\frac{x^3+2x^2-x-2}{2x^3-x-x^2}=\frac{1+2-1-2}{2-1-1}=\frac{0}{0}[/m]
Неопределенность
Раскладываем на множители и числитель и знаменатель:
[m]=\lim_{x \to 1}\frac{(x^2-1)(x+2)}{(x-1)(2x^2+x)}=[/m]
сокращаем на (х-1)
[m]=\lim_{x \to 1}\lim_{x \to 1}\frac{(x+1)(x+2)}{2x^2+x}=\frac{(1+1)(1+2)}{2+1}=2[/m]
3
[m]\lim_{x \to \infty }\frac{8x^4+3x^2-5}{1-2x^4}=\frac{∞}{-∞}[/m]
Неопределенность
Делим числитель и знаменатель на x^4:
[m]=\lim_{ \to \infty }\frac{\frac{8x^4+3x^2-5}{x^4}}{\frac{1-2x^4}{x^4}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^4 и
каждое слагаемое знаменателя делим на x^4:
[m]\lim_{ \to \infty }\frac{\frac{8x^4}{x^4}+\frac{3x}{x^4}-\frac{5}{x^4}}{\frac{1}{x^4}-\frac{2x^4}{x^4}}=[/m]
[m]\lim_{ \to \infty }\frac{8+\frac{3}{x^3}-\frac{5}{x^4}}{\frac{1}{x^4}-2}=\frac{8+0-0}{0-2}=-4[/m]
4.
[m]\lim_{x \to \infty }\frac{7x^{10}-11x+2}{(1+x)^{10}}=\frac{∞}{∞}[/m]
Неопределенность
Делим числитель и знаменатель на x^10:
[m]=\lim_{ \to \infty }\frac{\frac{7x^{10}-11x+2}{x^{10}}}{\frac{(1+x)^{10}}{x^{10}}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^(10)
[m]=\lim_{ \to \infty }\frac{\frac{7x^{10}}{x^{10}}-\frac{11x}{x^{10}}+\frac{2}{x^{10}}}{(\frac{1+x}{x})^{10}}=[/m]
[m]=\lim_{ \to \infty }\frac{7-\frac{11}{x^9}+\frac{2}{x^{10}}}{(\frac{1}{x}+1)^{10}}=\frac{7-0+0}{(0+1)^{10}}=7[/m]
Решения к другим задачам здесь не напишу. Выставляйте отдельными вопросами....