Задача 552 а) Ре­ши­те дан­ное урав­не­ние...

slava191

01.02.2014

а) Ре­ши­те дан­ное урав­не­ние 2cos^2x+2sin2x=3.
б) Ука­жи­те корни дан­но­го урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку [-3Pi/2; -Pi/2]

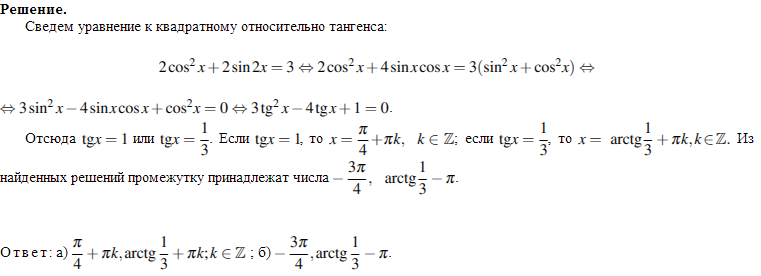
Ответ: в решение