Задача 55197 Добрый день!) Помогите пожалуйста Пример...
Условие
Помогите пожалуйста
Пример почти решен осталось одно действие.
Сам не смог)
Пример на фото)
Заранее спасибо)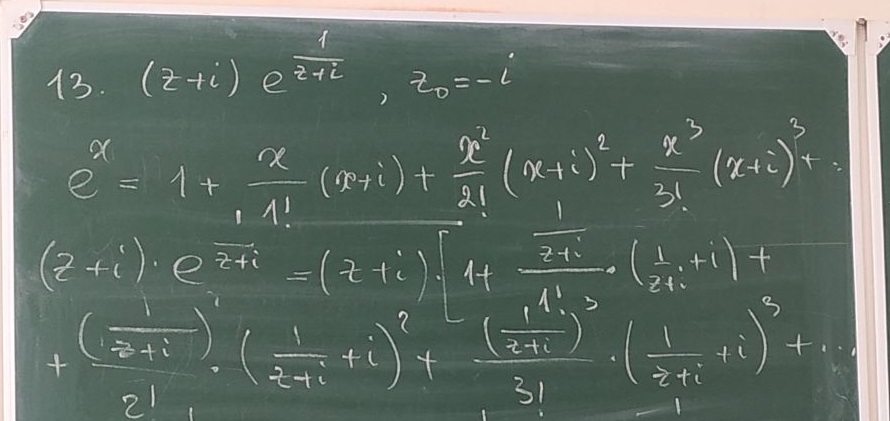
Решение
[m]e^{\frac{1}{z}}=1+\frac{1}{1!}\cdot (\frac{1}{z})+\frac{1}{2!}\cdot (\frac{1}{z})^2+...\frac{1}{n!}\cdot (\frac{1}{z})^{n}+...[/m]
[m]z\cdot e^{\frac{1}{z}}=z+\frac{1}{1!}\cdot (\frac{1}{z})\cdot z+\frac{1}{2!}\cdot (\frac{1}{z})^2\cdot z+...\frac{1}{n!}\cdot (\frac{1}{z})^{n}\cdot z+...[/m]
[m]z\cdot e^{\frac{1}{z}}=z+\frac{1}{1!}+\frac{1}{2!}\cdot (\frac{1}{z})+...\frac{1}{n!}\cdot (\frac{1}{z})^{n-1}+...[/m]
[m](z+i)\cdot e^{\frac{1}{z+i}}=(z+i)+1+\frac{1}{2!}\cdot \frac{1}{(z+i)}+...\frac{1}{n!}\cdot \frac{1}{(z+i)^{n-1}}+...[/m]
Главная часть ряда Лорана содержит одно слагаемое:
[m](z+i)[/m]
остальные [m]1+ \frac{1}{2!}\cdot \frac{1}{(z+i)}+...\frac{1}{n!}\cdot \frac{1}{(z+i)^{n-1}}+...[/m]
[m]1\cdot (z+i)^{0}+ \frac{1}{2!}\cdot(z+i)^{-1}+...+\frac{1}{n!}\cdot (z+i)^{-(n-1)}+...[/m]
записать с помощью знака суммы:
∑ ^(0)_( ∞) [m]\frac{1}{(n+1)!}\cdot (z+i)^{-n}[/m]