Задача 55137 исследовать функцию и построить график: ...

Эдуард_192960440

29 октября 2020 г. в 17:06

исследовать функцию и построить график: y = 2x³ – 9x² + 12x – 9

exponenta

29 октября 2020 г. в 18:33

★

y=2x³–9x²+12х–9

Область определения (– ∞ ;+ ∞ )

Функция непрерывна, так как является многочленом

y`=(2x<sup>3</sup>–9x<sup>2</sup>+12х–9)`

y`=6x²–18x+12

y`=0

6x²–18x+12=0

x²–3x+2=0

D=(–3)²–4·2=1

x=$\frac{3\pm1}{2}$

x₁=1; x₂=2

Расставляем знак производной ( производная y`=6x²–18x+12 – квадратичная функция, графиком этой функции является парабола, ветви вверх, поэтому на (1;2) производная отрицательна, на двух остальных – положительна):

__+__ (1) __–___ (2) __+__

y`>0 на (– ∞ ;1) и на (2;+ ∞ ), значит функция возрастает

y`< 0 на (1 ;12), значит функция убывает

х=1 – точка максимума, производная меняет знак с + на –

у(1)=2·1³–9·1²+12·1–9=–4


х=2 – точка минимума, производная меняет знак с – на +

y(2)=2·2³–9·2²+12·2–9=–5



y``=(6x²–18x+12)`

y``=12x–18

y``=0

12x–18=0

x=1,5– точка перегиба, вторая производная меняет знак с – на +

Функция выпукла вверх на ( – ∞ ;1,5) и выпукла вниз на (1,5;+ ∞ )


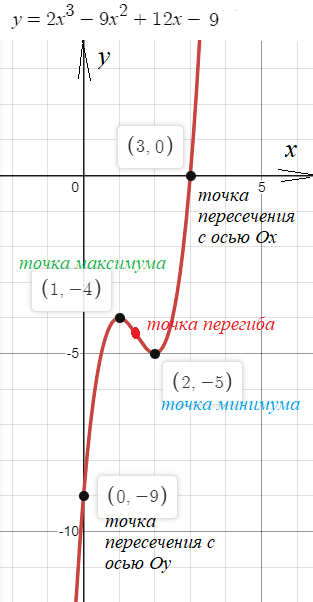
См. график на рис .