Задача 53541 ...

5f5f7f31116bb85615e04ab0

21.09.2020 21:29:00

Найдите все [b]а[/b], при которых неравенство

2aх + 2sqrt(2x+3) - 2x + 3a - 5 < 0

выполняется для всех x ∈ [-1; 3].

5f3ea7e3faf909182968ddd9

21.09.2020 21:58:15

★

[m] 2ax+3a+2\sqrt{2x+3}-(2x+3)+2<0[/m]

[m] (2x+3)a+2\sqrt{2x+3}-(2x+3)-2<0[/m]

Замена переменной:

[m]2x+3=t[/m]

[m]ta+2\sqrt{t}-t-2 <0[/m]

[m]ta<t+2-2\sqrt{t} [/m]

t>0

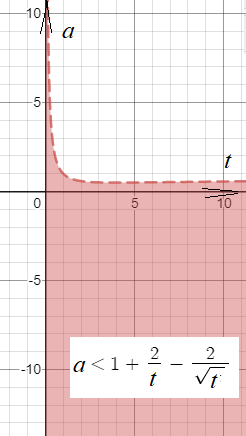
[m]a<1+\frac{2}{t}-\frac{2}{\sqrt{t}} [/m]

-1 ≤ x ≤ 3 ⇒ -2 ≤ 2x ≤ 6 ⇒ 1 ≤ 2x+3 ≤ 9

Пока только так...

Графически на плоскости tОа:
t ∈ [1;9]

t=1 ⇒ a=1
t=9 ⇒ a=1+(2/9)-(2/3)=(1/3)+(2/9)=(3/9)+(2/9)=5/9

t ∈ [1;9] ⇒ a ∈ [5/9;1]

О т в е т. (5/9;1)