Задача 53442 Найти все a, при которых уравнение...

5f282cfba9074b3a3bc0f013

16.09.2020 11:31:35

Найти все a, при которых уравнение sqrt(1-4x)*ln(9x^2-a^2)=sqrt(1-4x)*ln(3x+a) имеет ровно одно решение.

5f3ea7e3faf909182968ddd9

16.09.2020 12:43:11

★

[m]\sqrt{1-4x}\cdot ln(9x^2-a^2)=\sqrt{1-4x}\cdot ln(3x+a)[/m]

ОДЗ:
[m]\left\{\begin{matrix}1-4x \geq 0 \\9x^2-a^2> 0\\3x+a > 0\end {matrix}\right.[/m][m]\left\{\begin{matrix}1-4x \geq 0 \\3x-a>0\\3x+a > 0\end{matrix}\right.[/m]

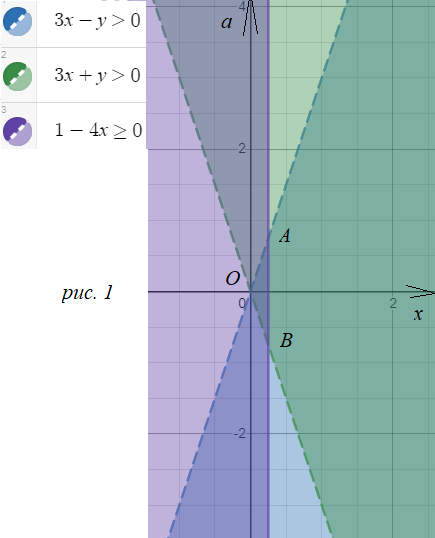
Строим область в системе координат [i]хОа[/i] ( см. рис. 1)

ОДЗ - треугольник OAB, причем стороны OA и OB не входят в ОДЗ ( изображены пунктирной линией)

[m]\sqrt{1-4x}\cdot ln(3x-a)\cdot (3x+a)-\sqrt{1-4x}\cdot ln(3x+a)=0[/m]

В условиях ОДЗ: [m] ln(3x-a)\cdot(3x+a)=ln(3x-a)+ln(3x+a)[/m]

[m]\sqrt{1-4x}\cdot ln(3x-a)+\sqrt{1-4x}\cdot ln(3x+a)-\sqrt{1-4x}\cdot ln(3x+a)=0[/m]

[m]\sqrt{1-4x}ln (3x+a)=0[/m]

Произведение равно 0 когда хотя бы один из множителей равен 0, а другой при этом не теряет смысла.

С учетом ОДЗ:

[m]\left\{\begin{matrix}1-4x = 0\\1-4x\geq 0 \\3x-a>0\\3x+a > 0\end{matrix}\right.[/m] или[m]\left\{\begin{matrix}ln(3x-a)=0\\ 1-4x \geq 0 \\3x-a> 0\\3x+a >0\end{matrix}\right.[/m]

[m]\left\{\begin{matrix}1-4x = 0\\1-4x\geq 0 \\3x-a> 0\\3x+a > 0\end{matrix}\right.[/m] или[m]\left\{\begin{matrix}3x-a=1\\ 1-4x \geq 0 \\3x-a> 0\\3x+a > 0\end{matrix}\right.[/m]


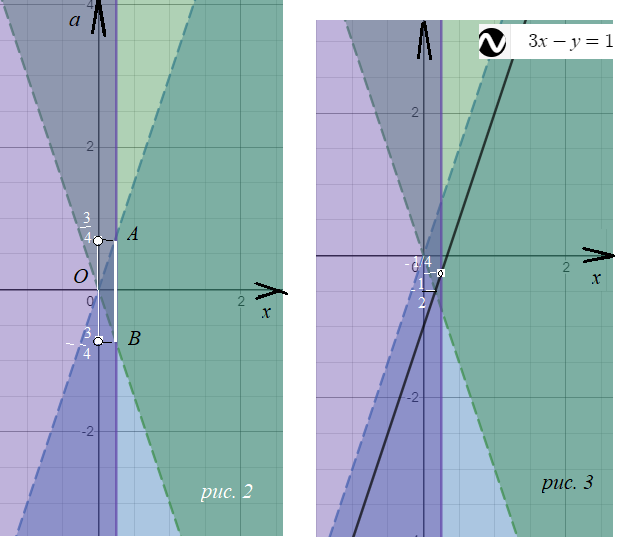
Строим каждую область в системе координат [i]хОа[/i]

cм. рис. 2 и рис. 3

Первая система имеет решение x=1/4 при a ∈ (-3/4; 3/4):

3x-a=0
x=1/4 ⇒ a=3/4

3x+a=0
x=1/4 ⇒ a=-3/4

Вторая система имеет решение при a ∈ (-1/2; -1/4)
[m]\left\{\begin{matrix}3x-a=1\\3x+a=0\end{matrix}\right.[/m] [m]\left\{\begin{matrix}3x-a=1\\1-4x=0\end{matrix}\right.[/m]

[m]\left\{\begin{matrix}x=\frac{1}{6}\\a=-\frac{1}{2}\end{matrix}\right.[/m] [m]\left\{\begin{matrix}a=-\frac{1}{4}\\x=\frac{1}{4}\end{matrix}\right.[/m]


О т в е т. (-3/4;-1/2] U [-1/4; 3/4)