Задача 52948 В июле 2026 года планируется взять...

slava191

2020-07-31 22:28:42

В июле 2026 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— в июле 2027, 2028 и 2029 годов долг остаётся равным 220 тыс. рублей;

— выплаты в 2030 и 2031 годах равны;

— к июлю 2031 года долг будет выплачен полностью.

Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.

sova

2020-08-01 08:31:36

★

Cумма кредита S=220 тыс руб.

Каждый январь начисляются проценты на остаток.
r%= 0,01*r

Обозначим
[b]1+0,01*r= k[/b]

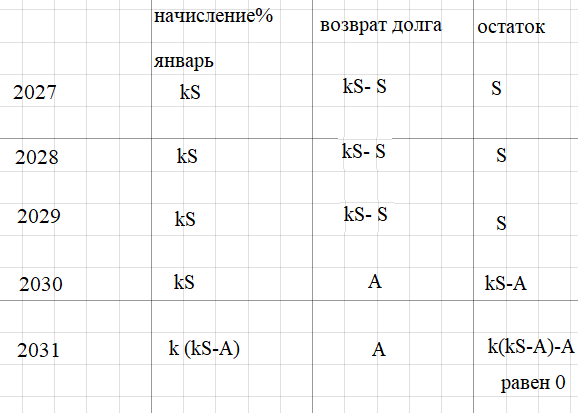
( cм схему начисления и остатки к таблице)

Уравнение 1:
k*(kS-A)-A=0

Уравнение 2:
3*(kS-S)+2A=420
S=220

Решаем систему уравнений:

[m]\left\{\begin{matrix} k(220k-A)-A=0\\ 3(220k-220)+2A=420 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} 220k^2=A(k+1)\\ 660k-660+2A=420 \end{matrix}\right.[/m]

[m]\left\{\begin{matrix} A=\frac{220k^2}{k+1}\\ 660k+2\frac{220k^2}{k+1} =1080 \end{matrix}\right.[/m] [m]\left\{\begin{matrix} A=\frac{220k^2}{k+1}\\ 66k(k+1)+44k^2 =108(k+1)\end{matrix}\right.[/m]

[m]\left\{\begin{matrix} A=\frac{220k^2}{k+1}\\ 55k^2-21k-54=0\end{matrix}\right.[/m] D=21^2-4*55*(-54)=441+11880=12321=[b]111^2[/b]

k=1,2 второй корень отрицательный

1+0,01r=k ⇒ 1+0,01r=1,2 ⇒ 0,01*r=0,2 ⇒ r=20%

О т в е т.[b] 20%[/b]

___