Задача 529 Найти все значения параметра a, при...

slava191

29.01.2014

Найти все значения параметра a, при которых функция f(x) = x^2 - |x-a^2| - 9x имеет хотя бы одну точку максимума.

Раскроем модуль:

При x <= a^2: f(x) = x^2 - 8x - a^2,
при x > a^2: f(x) = x^2 - 10x + a^2.

Производная левой части: f'(x) = 2x - 8
Производная правой части: f'(x) = 2x - 10

И левая, и правая части могут иметь только минимум. Значит, единственный максимум у функции f(x) может быть в том и только в том случае, если в точке x=a^2 левая часть возрастает (то есть 2x-8 > 0), а правая — убывает (то есть 2x-10 < 0).

То есть, получаем систему:
2x-8 > 0
2x-10 < 0
x = a^2

откуда
4 < a^2 < 5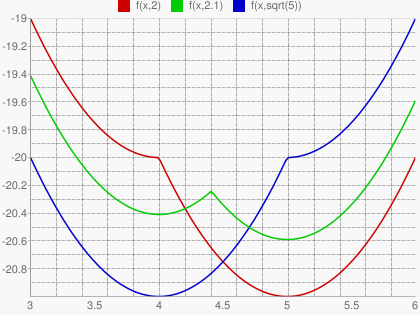

Ответ: (-sqrt(5); -2) ? (2; sqrt(5))