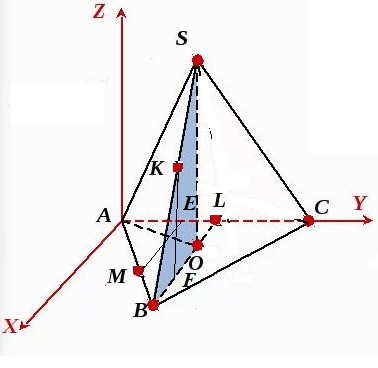
Задача 52853 На ребрах SB и AB правильной треугольной...

slava191

11 июля 2020 г. в 18:57

На ребрах SB и AB правильной треугольной пирамиды SABC отметили соответственно точки K и M так, что SK : KB = 5 : 6 и AM : MB = 7 : 2. Ребрами пирамиды AB = 9, SC = √43.
а) Докажите, что плоскости CKM и ABC перпендикулярны.
б) Найдите объем пирамиды CBMK.

sova

12 июля 2020 г. в 10:42

Пирамида – правильная.
АВ=ВС=АС=9
SA=SB=SC=√43
О– центр вписанной и описанной окружностей

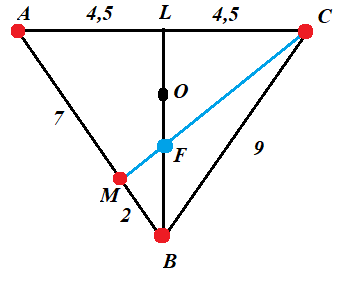
AL=LC=9/2
BL=h _{Δ ABC}=9√3/2
BO=R=9√3/3=3√3
LO=r=9√3/6


Из Δ SOB
SO²=SB²–BO²=(√43)²–(3√3)²=43–27=16
SO=4

Проекция точки К на плоскость АВС – точка F

Точка F лежит на высоте ВL треугольника АВС

Докажем, что точка F лежит на отрезке СМ

Составим уравнение прямой СМ на плоскости, как прямой, проходящей через две точки:

[m]\frac{x-0}{\frac{7\sqrt{3}}{2}}=\frac{y-9}{\frac{7}{2}-9}

[m]-11x=7\sqrt{3}y-63sqrt{3}[/m]

Найдем координаты точки F.

Из подобия Δ SBO и Δ KBF

BF=(6/11)BO=(18√3/11)

KF=(6/11)·SO=24/11

LF=BL–BF=(9√3/2)–(18√3/11)=9√3·((1/2)–(2/11))=(7/22)·9√3=63√3/22

F(63√3/22;9/2;0)

Подставим в уравнение прямой СМ:

[m]-11\cdot \frac{63\sqrt{3}}{22}=7\sqrt{3}\cdot \frac{9}{2}-63sqrt{3}[/m]

верно.
⇒ F лежит на СM
и

KF ⊥ пл АВС

Плоскость CКМ проходит через KF ⇒ пл СКМ ⊥ АВС

б)

V_{пирамиды СВМК}=[m]\frac{1}{3}S_{ CBM}\cdot KF=

\frac{1}{3}\cdot\frac{1}{2} \cdot 2\cdot 9\cdot \frac{\sqrt{3}}{2}\cdot \frac{24}{11}=\frac{36\sqrt{3}}{11}[/m]

____________________________

2 способ: координатный

Из подобия треугольников АВL и АМЕ
MЕ=7√3/2

A(0;0;0)
C(0;9;0)
В(9√3/2; 9/2;0)
M(7√3/2; 7/2;0)

O(9√3/6; 9/2;0)

S(9√3/6; 9/2;4)


F(63√3/22;9/2;0)


K(63√3/22;9/2;24/11)

Уравнение плоскости ABC:

z=0

n_ABC=(0;0;1)

Уравнение плоскости СКМ:
C(0;9;0)
M(7√3/2; 7/2;0)

K(63√3/22;9/2;24/11)


[m]\begin{vmatrix} x& y-9 &z \\ \frac{7\sqrt{3}}{2} &\frac{7}{2}-9 & 0\\ \frac{63\sqrt{3}}{22} &\frac{9}{2}-9 &\frac{24}{11} \end{vmatrix}=0[/m]

⇒

[m]-12x-\frac{63\sqrt{3}}{4}z+\frac{11}{2}\cdot (\frac{63\sqrt{3}}{22})z-\frac{24}{11}\cdot \frac{7\sqrt{3}}{2}\cdot (y-9)=0[/m]

[m]-12x-\frac{24}{11}\cdot \frac{7\sqrt{3}}{2}\cdot y-\frac{24}{11}\cdot \frac{7\sqrt{3}}{2}\cdot9=0[/m]


n_CKM=(–12; [m]\frac{84\sqrt{3}}{2}[/m];0)


n_ABC·n_CKM=–12·0+[m]\frac{84\sqrt{3}}{2}[/m]·0+0·1 =0

Векторы n_ABC ⊥ n_CKM ⇒

пл АВС ⊥ пл СМК

б

2 способ: координатный

C(0;9;0)
В(9√3/2; 9/2;0)
M(7√3/2; 7/2;0)
K(63√3/22;9/2;24/11)


V_{пирамиды СВМК}=[m]\frac{1}{6}\cdot |(\vec{CB},\vec{CM},\vec{CK})|[/m]


[m](\vec{CB},\vec{CM},\vec{CK})=\begin{vmatrix}\frac{9\sqrt{3}}{2} & \frac{9}{2}-9 &0 \\ \frac{7\sqrt{3}}{2} &\frac{7}{2}-9 & 0\\ \frac{63\sqrt{3}}{22} &\frac{9}{2}-9 &\frac{24}{11} \end{vmatrix}=\frac{24}{11}\cdot \begin{vmatrix}\frac{9\sqrt{3}}{2} & \frac{9}{2}-9 \\ \frac{7\sqrt{3}}{2} &\frac{7}{2}-9 \end{vmatrix}=[/m]

[m]=-\frac{24\cdot 9\sqrt{3}}{11}[/m]

V_{пирамиды СВМК}=[m]\frac{1}{6}\cdot|-\frac{24\cdot 9\sqrt{3}}{11}|= \frac{36\sqrt{3}}{11}[/m]