Задача 52530 Найдите все значения a, при каждом из...

mihalevapolina

2020-06-18 10:01:29

Найдите все значения a, при каждом из которых система неравенств
[m]
\begin{cases}
4|x| + |a| \leq 4, \\
x^2 + 2x \leq a + 3
\end{cases}
[/m]
имеет хотя бы одно решение.

sova

2020-06-18 16:25:02

★

Находим координаты точки персечения графиков в третьей четверти:
x <0; a<0
|x|=-x
|a|=-a

{4(-x)-a=4 ⇒ a=-4x-4
{x^2+2x=a+3

x^2+2x=-4x-4+3

x^2+6x+1=0
D=36-4=32
x_(1)=(-6-4sqrt(2))/2=-3-2sqrt(2); x_(2)=(-6+4sqrt(2))/2=-3+2sqrt(2);

a_(1)=-4(-3-2sqrt(2))-4=12+8sqrt(2)-4=8+8sqrt(2)>0 не удовл условию a<0

a_(2)=-4*(3+sqrt(2))-4=[b]8-8sqrt(2)[/b]<0


О т в е т. [8-8sqrt(2);4]

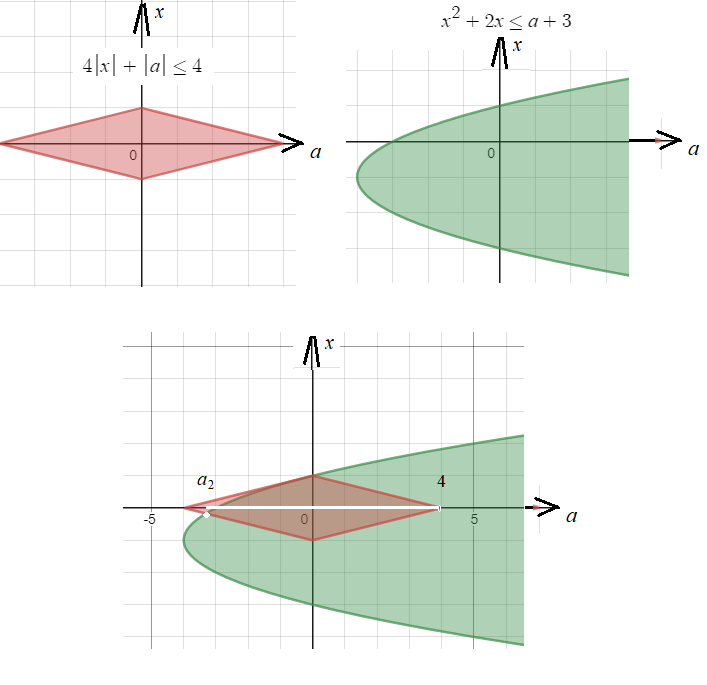
Cм графики в системе координат аОх