Задача 52310 ...

tunerokk

9 июня 2020 г. в 16:33

а) Решите уравнение 2 cos³ x = sin (π/2 – x) + 0,5 sin 2x.

б) Найдите корни уравнения, принадлежащие промежутку (–π/2; 5π/2).

sova

9 июня 2020 г. в 18:42

sin2x=2sinx·cosx

По формулам приведения:
sin((π/2)–x)=cosx

Уравнение:
2cos³x=cosx+sinx·cosx

2cos³x–cosx–sinx·cosx=0

cosx·(2cos²x–sinx–1)=0

cosx·(2–2sin²x–sinx–1)=0

cosx·(2sin²x+sinx–1)=0

cosx=0 или 2 sin²x+sinx–1=0

x=(π/2)+πn, n ∈ Z или D=1–4·2·(–1)=9 корни 1/2 и –1 ⇒

sinx=1/2 ⇒ x=(–1)^k·(π/6)+πk, k ∈ Z

sinx=–1 ⇒ x=(–π/2)+2πm, m ∈ Z

О т в е т.
а) (π/2)+πn, n ∈ Z; (–1)^k·(π/6)+πk, k ∈ Z

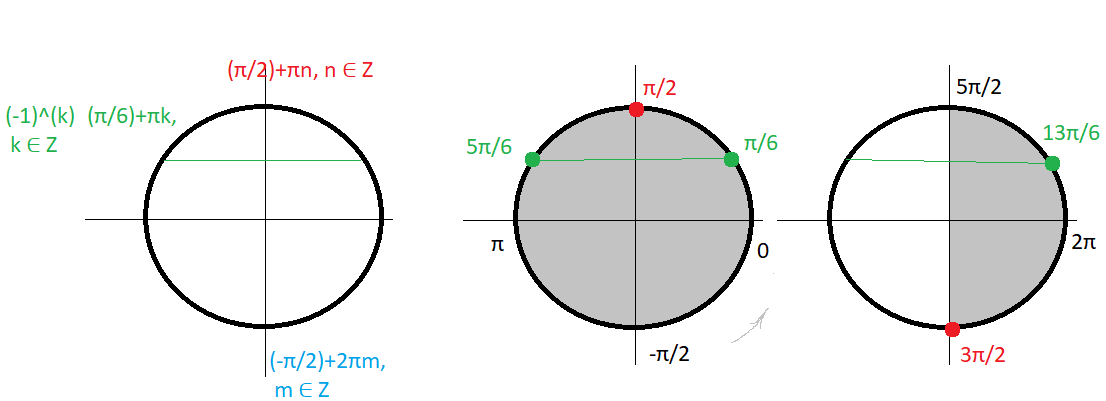
б)(π/2); (3π/2) ∈ (–π/2; 5π/2)
(π/6); (5π/6);(π/6)+2π=(13π/6) ∈ (–π/2; 5π/2)