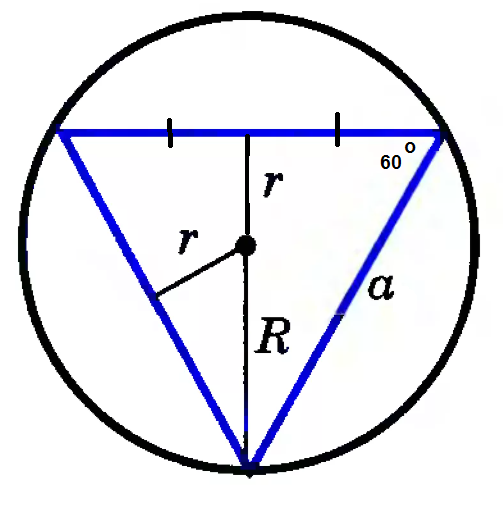
Задача 50124 Внутрь круга радиуса R наудачу брошена...

vk549619092

2020-05-14 08:52:25

Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника. Предполагается, что вероятность попадания точки в треугольник пропорциональна площади треугольника и не зависит от его расположения относительно круга.

sova

2020-05-14 09:54:06

★

Геометрическая вероятность

p=S_( Δ)/S_(круга)

S_(круга)=π*R^2

R_(описанной окр)=a*sqrt(3)/3 ⇒ a=R*sqrt(3)


S_( Δ)=(1/2)a^2*sin60 ° =a^2sqrt(3)/4=3R^2sqrt(3)/4


p=(3sqrt(3))/(4π)