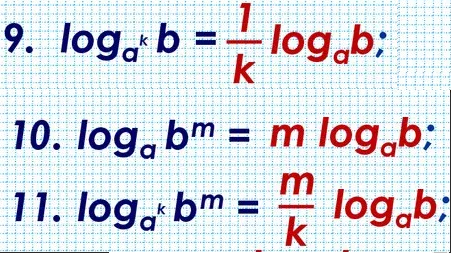Задача 49513 a) Решите уравнение log2(4x^4 + 28) - 2...

missdiana

2020-05-07 10:37:44

a) Решите уравнение log2(4x^4 + 28) - 2 + log2sqrt(5x^2+1);

б) Найдите все корни этого yравнения, принадлежащие отрезку [-9/5 ; 7/5].

sova

2020-05-07 10:51:37

★

4x^4+28 >0 при любом х
5x^2+1>0 при любом х

log_(2)(4x^4+28)=log_(2)(4*(x^4+7))=log_(2)4+log_(2)(x^4+7)=2+log_(2)(x^4+7)

log_(sqrt(2))sqrt(5x^2+1)=log_(2)(5x^2+1) ( см. приложение формула 11)


Уравнение:
log_(2)(x^4+7)=log_(2)(5x^2+1) ⇒

x^4+7=5x^2+1 - биквадратное уравнение

x^4-5x^2+6=0

x^2=2 или x^2=3

x= ± sqrt(2); x= ± sqrt(3)

О т в е т.
а)± sqrt(2); ± sqrt(3).


б)
-9/5=-1,8
7/5=1,4

sqrt(2) ≈ 1,41 >1,4=7/5;
sqrt(3) ≈ 1,7 > 1,4=7/5

sqrt(2) ∉ [-9/5;7/5]
sqrt(3) ∉ [-9/5;7/5]

-sqrt(2) ≈ -1,41 >-1,8=-9/5
-sqrt(3) ≈ 1,7 > -1,8=-9/5

-sqrt(2) ∈ [-9/5;7/5]
-sqrt(3) ∈ [-9/5;7/5]

О т в е т б)-sqrt(2) ∈ [-9/5;7/5]:-sqrt(3) ∈ [-9/5;7/5]