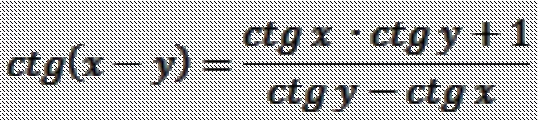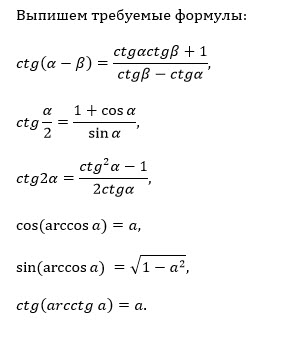Задача 49144 Вычислить...
Условие
Все решения
arccos[m]\frac{3}{5}[/m]= α ⇒ cos α =[m]\frac{3}{5}[/m]=0,6 и α ∈ [0;[m]\frac{\pi}{2}[/m]] угол в первой четверти
sin α =+ sqrt(1-cos^2 α )=sqrt(1-0,6^2)=0,8
arcctg (-[m]\frac{1}{2}[/m])= β ⇒ ctg β =-[m]\frac{1}{2}[/m]; β ∈ [[m]\frac{\pi}{2}[/m];π]
По условию задачи требуется вычислить
[m]ctg(\frac{1}{2}\alpha-2\cdot \beta)[/m]
cм (формулу в приложении)
Вычисляем:
[m]ctg(\frac{1}{2}\alpha)=ctg \frac{\alpha}{2}=\frac{1+cos \alpha}{sin\alpha} =\frac{1+0,6}{0,8} =2[/m]
Вычисляем:
[m]ctg2\beta= \frac{ctg^2\beta -1}{2ctg\beta} =\frac{(-\frac{1}{2})^2-1}{2\cdot (-\frac{1}{2})}=\frac{3}{4}[/m]
Итак,
[m]ctg(\frac{\alpha}{2}-2\cdot \beta)=\frac{2\cdot \frac{3}{4}+1}{\frac{3}{4}-2}=-2[/m]
О т в е т. -2
