Задача 47160 Найти радиус и интервал сходимости ряда;...
Условие
концах интервала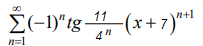
Решение
a_(n)=tg(11/4^n)
Ряд из модулей:
∑ a_(n)(x+7)^(n+1) - степенной ряд
R=lim_(n → ∞ )a_(n)/a_(n+1)=lim_(n → ∞ )tg(11/4^(n))/tg(11/4^(n+1))=[b]4[/b]
( применили следствие из [i]первого замечательного предела[/i]: tgx~x при x → 0)
tg (11/4^n )~(11/4^(n)) при n → ∞
tg (11/4^(n+1) )~(11/4^(n+1)) при n → ∞
(11/4^(n)) : (11/4^(n+1))=[b]4[/b]
Степенной ряд ∑ a_(n)x^(n) имеет радиус сходимости R
т.е сходится в интервале (-R;R)
Cтепенной ряд ∑ a_(n)(x-x_(o))^(n)имеет радиус сходимости R
т.е сходится в интервале (x_(o)-R;x_(o)+R)
В задаче
R= 4
x_(o)=-7
(-7-4; -7+4)=(-11;:-3)- интервал сходимости