Задача 46984 Помогите решить Решить однородное...
Условие
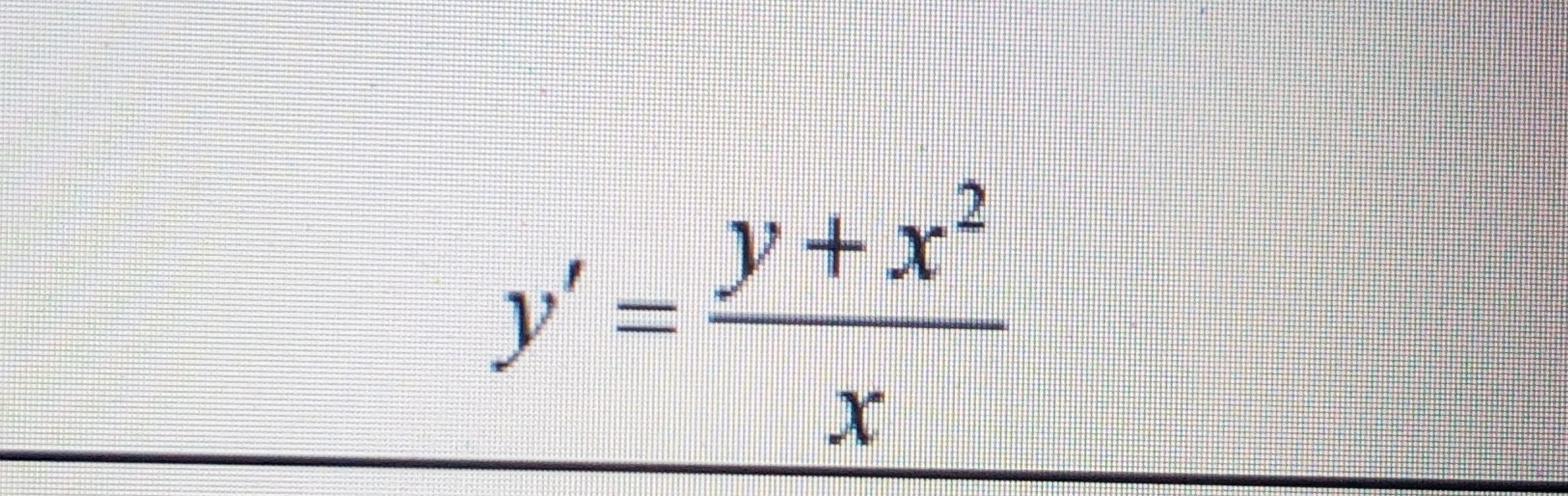
предмет не задан
825
Решение
★
Однородное - правая часть функция от дроби (y/x) или (x/y)
Если справа почленно поделить на х
получим
y`=(y/x)+x
y`-(1/x)*y=x
Это линейное первого порядка.
Решаем методом Бернулли
Решение в виде
y=u*v
Находим
y`=u`*v+u*v`
Подставляем в уравнение:
u`*v+u*v`-(1/x)*u*v=x
Сгруппируем:
u`*v+u(v`-(1/x)*v)=2x^3
Выбираем функцию v так,чтобы
v`-(1/x)*v=0
Решаем уравнение с разделяющимися переменными
v`-(1/x)*v=0 ⇒ dv/v=1dx/x ⇒ ∫ dv/v=∫ dx/x ⇒ ln|v|=ln|x| ⇒ [b]v=x[/b]
Тогда данное уравнение принимает вид
u`*v+u*0=2x^3
u`*x=x
u`=1
u=x+C
y=u*v=(x+C)*x
[b]y=x^2+Cx[/b]

