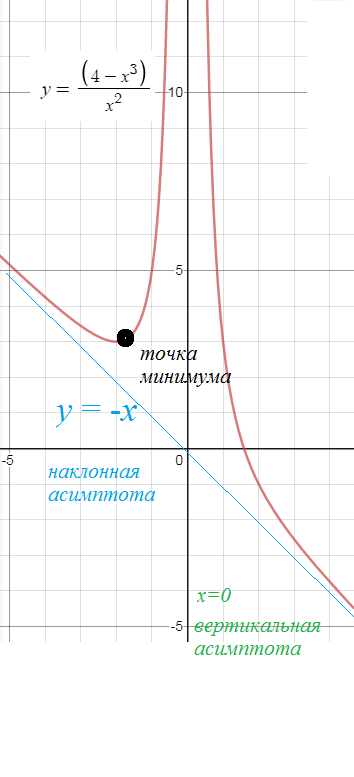
Задача 46447 провести полное исследование и построить...

vk34347336

8 апреля 2020 г. в 21:49

провести полное исследование и построить график функции у=(4–х³)/x²

sova

8 апреля 2020 г. в 21:56

★

1) D(y)=(–∞;0)U(0;+ ∞)

точка x=0 не входит в область определения
Находим пределы слева и справа:
f(–0)=lim_x→–0f(x)=+ ∞
f(+0)=lim_x→+0f(x)=+ ∞

Они бесконечные, значит

х=0 – точка разрыва второго рода

х=0 – вертикальная асимптота.

2) Функция не является ни четной, ни нечетной.
у(–х)=(4–(–х)³)/(–x)²=(4+x³)/x²

y(–x)≠y(x)
y(–x)≠–y(x)


3)lim_{x→ +∞})f(x)=–∞
lim_x→–∞f(x)=+∞.

Горизонтальных асимптот нет

4)
Наклонная асимптота это прямая y=kx+b

Находим

k=lim_{x→ ∞} (4–x³)/x³=–1

Находим

b=lim_x→∞ (f(x)–x)=lim_{x→+ ∞} 1/x²=0

y=–x – наклонная асимптота.

5) f(x)=0
4–x³=0
x=∛4 – точка пересечения с осью Ох

f(0)=не существует.
Точек пересечения с осью Оу нет.

Исследование функции с помощью производной

6) y=(4/x²)–x

y`=4·(–2)·x^–3–1

y`=(–8/x³)–1

y`=0
x=2 – точка минимума, производная меняет знак с – на +

Знак производной:
_____–__ (–2 ) __+__ (0) __+ _

y`>0 на (–2; 0)
функция возрастает на (–2; 0)

y`<0 на (– ∞ ;–2) и на (0;+ ∞ )
функция убывает на (– ∞ ;–2) и на (0;+ ∞ )

у2)=(4–(–2)²)/2²=2


7)y``=–8·(–3)x^–4

y``=24/x⁴ >0 при всех х≠0

Функция выпукла вниз

Точек перегиба нет.