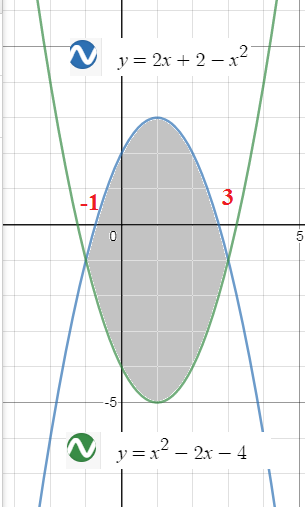
Задача 46294 Вычисли площадь фигуры, ограниченной...

vk332222239

2020-04-07 12:35:58

Вычисли площадь фигуры, ограниченной линиями: y=x^2-2x-4,
y=2x+2-x^2

sova

2020-04-07 12:51:08

★

Находим абсциссы точек пересечения:
x^2-2x-4=2x+2-x^2

2x^2-4x-6=0

x^2-2x-3=0

D=16

x_(1)=-1; x_(2)=3

S= ∫ ^(b)_(a)(f(x)-g(x)dx

S=∫ ^(3)_(-1)(2x+2-x^2-(x^2-2x-4))dx=


=∫ ^(3)_(-1)(6+4x-2x^2)dx=(6x+2x^2-(2/3)x^3)|^(3)_(-1)=

=6*(3-(-1))+2*(3^2-(-1)^2)-(2/3)*(3^3-(-1)^3)=


=24+16-(2/3)*28=[b]64/3[/b]