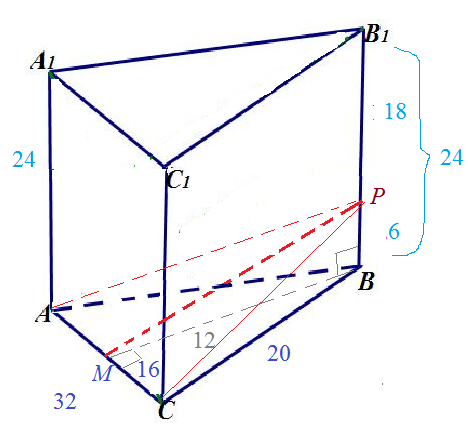
Задача 45743 Основанием прямой треугольной призмы...

slava191

2020-04-01 12:22:21

Основанием прямой треугольной призмы АВСА1В1С1 является равнобедренный треугольник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка P принадлежит ребру ВВ1 причём ВР : РВ1 = 1:3.

а) Пусть М — середина АС. Докажите, что прямые МР и А1C1 перпендикулярны.

б) Найдите тангенс угла между плоскостями А1B1C1 и АСР. [14п11]

sova

2020-04-02 12:37:11

★

а)
Призма АВСА1В1С1 - прямая, значит АА_(1); ВВ_(1) и СС_(1) перпендикулярны пл. оснований.

Значит перпендикулярны любой прямой, лежащей в этих плоскостях, в частности
ВВ_(1) ⊥ AB и ВВ_(1) ⊥ AC.

ВВ_(1) ⊥ AB ⇒ MB- проекция АР на пл АВС

Так как треугольник АВС - равнобедренный, его медиана BM одновременно и высота.
BM ⊥ АС

По теореме о трех перпендикулярах

АС ⊥ MP

A_(1)C_(1) || AC ⇒ A_(1)C_(1) ⊥ MP. Что и требовалось доказать.

б)
причём ВР : РВ1 = 1:3,
значит 24:4=6
ВР=[b]6[/b]; РВ1 = [b]18[/b]

Так как треугольник АВС - равнобедренный, его медиана BM одновременно и высота.
Треугольник ВМС - прямоугольный, ВС=20; МС=АС/2=32/2=16
ВМ=[b]12[/b]


пл А1В1С1 || пл АВС.

∠ PMB - линейный угол двугранного угла между пл. АВС и АРС
по определению: BM ⊥ AС и PM ⊥ AC

tg∠ PMB=PB/BM=6/12=1/2

Значит, тангенс угла между между плоскостями А1B1C1 и АСР равен 1/2

О т в е т. 1/2