Задача 45742 Дан куб ABCDA1B1C1D1. а) Докажите, что...
Условие
а) Докажите, что сечение куба плоскостью, проходящей через центр куба перпендикулярно диагонали АС1 является правильным шестиугольником.
б) Найдите угол между прямой АС1 и плоскостью ВСС1. [14п10]
Решение
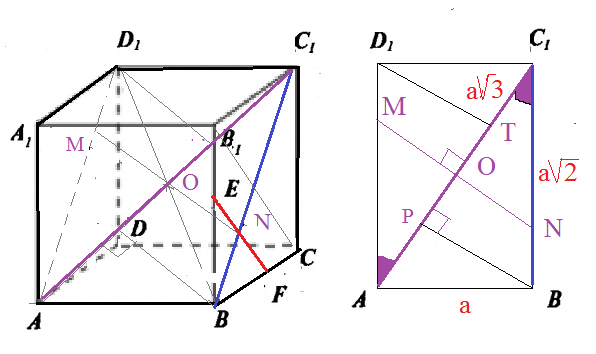
a) Диагональ АС_(1) принадлежит плоскости AD_(1)C_(1)B
В прямоугольник AD_(1)C_(1)B:
AD_(1)=BC_(1)=[b]a[/b]*sqrt(2)
AC_(1)=[b]a[/b]*sqrt(3)
Центр куба точка О - точка пересечения диагоналей AC_(1) и BD_(1)
В прямоугольнике AD_(1)C_(1)B:
через точку О - проводим [b]MN[/b] ⊥ AC_(1).
АО=ОС_(1) и ∠ D_(1)AO= ∠ OC_(1)N ⇒ АМ=С_(1)N; D_(1)N=BN
BP=a*sqrt(2)/sqrt(3) (высота прямоугольного треугольника АВС_(1))
По теореме Пифагора АР^2=AB^2-BP^2=a^2-(a*sqrt(2)/sqrt(3))^2=a^2/3 ⇒
AP=a*sqrt(3)/3
Аналогично С_(1)Т=a*sqrt(3)/3;
Тогда PT=AC_(1)-AP-CT=a*sqrt(3)/3
O-середина PT ⇒PO= OT=a*sqrt(3)/6
РО:ОС_(1)=[b]1:3 [/b]⇒ BN:NC_(1)=[b]1:3[/b]
Точка М ∈ грани АD_(1)D, N ∈ BB_(1)C
BN:NC1=[b]1:3[/b] ⇒ BN_(1):N_(1)C=[b]1:3[/b] и DM_(1):M_(1)A=[b]1:3[/b]
По теореме о 3-х перпендикулярах диагональ АС_(1) ⊥ B_(1)C, так как BC_(1)-проекция АС_(1) и BC_(1) ⊥ B_(1)C - диагонали квадрата ВB_(1)C_(1)С
Через точку N проводим EF || B_(1)C.
EF⊥ АС_(1)
и АС_(1) перпендикулярна двум пересекающимся прямым
MN и EF пл. MEF
пл. МЕF= α - искомая плоскость сечения.
Плоскость α пересекает грань BC_(1) ⊥ B_(1)C по отрезку ЕF
EF=(1/2)B_(1)C.=a*sqrt(2)/2
И так в каждой грани. Все шесть сторон сечения - параллельным соответствующим диагоналям граней куба и равны a*sqrt(2)/2
б)
tg ∠ АС_(1)B=AB/BC_(1)=[b]1/sqrt(2)=sqrt(2)/2[/b]
sin∠ АС_(1)B=AB/AC_(1)=1/sqrt(3)
cos∠ АС_(1)B=BC_(1)/AC_(1)=sqrt(2/3)
О т в е т. ∠ АС_(1)B=arctg [b]sqrt(2)/2[/b]
Есть решение cлучая а) координатным методом.
Не мое. Из интернета.
Диагонали BD_(1) и АС_(1) взаимозаменяемы.