Задача 45741 Основание прямой четырёхугольной призмы...
Условие
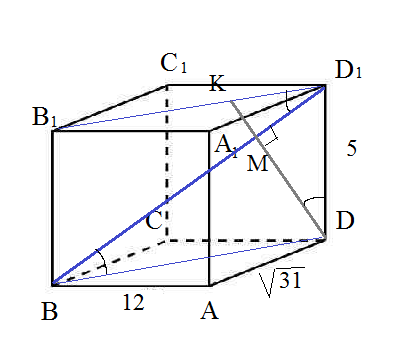
а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой BD1 делит отрезок B1D1 в отношении 1:6.
б) Найдите косинус угла между плоскостью, проходящей через точку D перпендикулярно прямой BD1 и плоскостью основания призмы. [14п9]
Решение
BD^2=AB^2+AD^2=12^2+(sqrt(31))^2=144+31=175
[b]BD=sqrt(175)[/b]
Прямые АС и B_(1)D_(1) расположены в параллельных плоскостях оснований АВСD и A_(1)B_(1)C_(1)D_(1).
Расстояние между ними есть длина общего перпендикуляра к ним.
Таким перпендикуляром является боковое ребро призмы.
AA_(1)=BB_(1)=CC_(1)=DD_(1)=5
Прямоугольные треугольники Δ D_(1)BD и KDD_(1) подобны по двум углам (равные углы отмечены на рисунке)
∠ MDB= ∠ DKD_(1) внутренние накрест лежащие при параллельных BD и B_(1)D_(1) и секущей KD
Из подобия: DD_(1):BD=KD_(1):DD_(1)
KD_(1)=[m]\frac{5\sqrt{7}}{7}[/m]
Тогда
B_(1)K=5sqrt(7)-[m]\frac{5\sqrt{7}}{7}[/m]=[m]\frac{30\sqrt{7}}{7}[/m]
[b]B_(1)K:KD_(1)=30:5=6:1[/b]
б)
∠ MDB - угол между плоскостью, проходящей через точку D перпендикулярно прямой BD1 и плоскостью основания призмы
∠ MDB= ∠ DKD_(1) внутренние накрест лежащие при параллельных BD и B_(1)D_(1) и секущей KD
Из Δ DKD_(1):
tg ∠ DKD_(1)=DD_(1):KD_(1)=5: [m]\frac{5\sqrt{7}}{7}=\sqrt{7}[/m]
tg∠ MDB=[m]\sqrt{7}[/m]
cos∠ MDB=[m]\frac{1}{\sqrt{1+tg^2\angle MDB}}=\frac{1}{8}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}[/m]
О т в е т. cos∠ MDB=[m]\frac{\sqrt{2}}{4}[/m]