Задача 45739 В правильной шестиугольной пирамиде...

slava191

2020-04-01 12:06:52

В правильной шестиугольной пирамиде SABCDEF боковые рёбра равны 2, а стороны основания — 1.

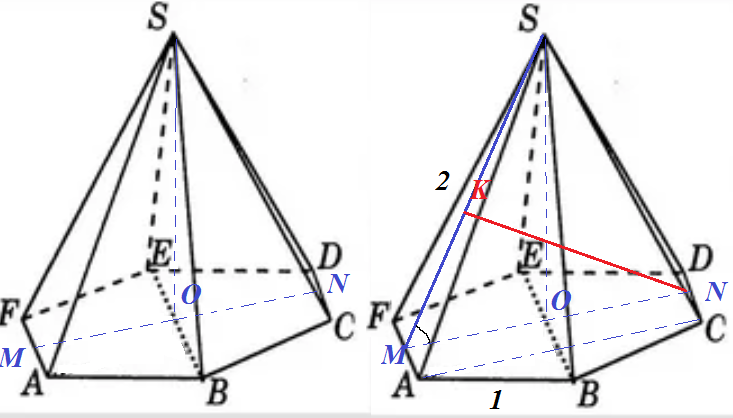
а) Докажите, что плоскость, проходящая через вершину В и середины рёбер AF и CD, перпендикулярна плоскости основания.

б) Найдите косинус угла между прямой АС и плоскостью SAF. [14п8]

sova

2020-04-01 17:17:13

★

Пусть М - середина АF; N - середина СD.

AF||CD||BE

ABEF и BCDE - равнобедренные трапеции.

Пусть O- [i]середина[/i] BD

Тогда MO ⊥ AF и NO ⊥ CD

Так как из точки О к параллельным прямым AF и CD можно провести только один перпендикуляр.
O ∈ MN

SO ⊥ пл. АВСDEF,
плоскость SMN пpоходит через перпендикуляр к другой плоскости, поэтому плоскости перпендикулярны.

б)

Прямая АС || MN

Угол между прямой и плоскостью равен углу между прямой и ее проекцией на плоскость.

Δ SMN - равнобедренный,

NK ⊥ SM, значит проекцией MN на пл. SAF является MK,
K ∈ SM

OM=sqrt(3)/2
SM^2=SA^2-AM^2=2^2-(1/2)=4-(1/4)=15/4
SM=sqrt(15)/2

cos ∠ SMO=OM/SM=sqrt(3)/2/sqrt(15)/2=1/sqrt(5)=[b]sqrt(5)/5[/b]