Задача 45517 a) Найдите корень уравнения...

slava191

2020-03-28 16:44:28

a) Найдите корень уравнения 2cos2x-12cosx+7 = 0

б) Отбор корней на промежутку [-Pi; 5Pi/2] (15)

sova

2020-03-28 17:28:38

★

а)
сos2x=2сos^2x-1;

2*(2cos^2x-1)-12cosx+7=0

4cos^2x-12cosx+5=0

D=(-12)^2-4*4*5=144-80=64

сosx=0,5 или сosx =2,5


сosx=0,5

[m]x=\pm arccos 0,5+2\pi n, n \in Z[/m] ⇒
[m]x=\pm \frac{\pi}{3}+2\pi n, n \in Z[/m]


cosx=2,5 - уравнение не имеет корней, -1 ≤ cosx ≤ 1

О т в е т. а)
[m]x=\pm \frac{\pi}{3}+2\pi n, n \in Z[/m]

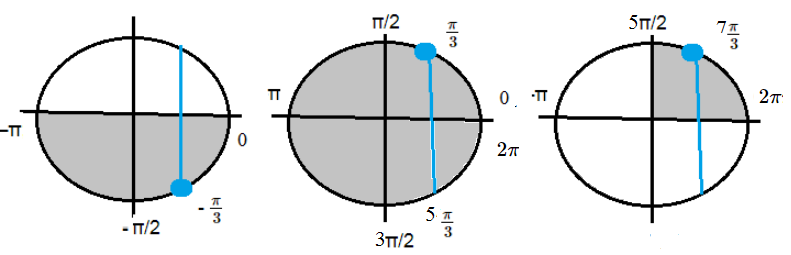
б) [–π; 5π/2] принадлежат корни:
[m]x=\pm \frac{\pi}{3}[/m]: [m]x= \frac{5\pi}{3}[/m]; [m]x= \frac{7\pi}{3}[/m] [–π; 5π/2]