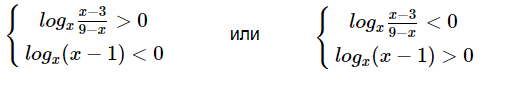Задача 45357 log x (x-3) - log x (9-x)/log x-1(x)<0...

bobrov223

2020-03-25 20:51:18

log x (x-3) - log x (9-x)/log x-1(x)<0

sova

2020-03-25 21:07:39

{x>0; x ≠ 1
{x-3>0 ⇒ x>3
{9-x>0 ⇒ x < 9
{x-1>0; x-1 ≠ 1 ⇒ x>1; x ≠ 2

x ∈ (3;9)

[m]log_{x}(x-3)-log_{x}(9-x)=log_{x}\frac{x-3}{9-x}[/m]

[m]\frac{log_{x}\frac{x-3}{9-x}}{log_{x-1}x}<0\Rightarrow log_{x}\frac{x-3}{9-x}\cdot log_{x}(x-1)<0 [/m]