Задача 45354 найти объем тела образованного вращением...
Условие
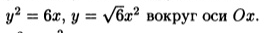
математика ВУЗ
852
Все решения
a=0; b=1
f(x)=sqrt(6x)
g(x)=sqrt(6)*x^2
f^2(x)=6x
g^2(x)=(sqrt(6)*x^2)^2=6x^4
V_(оси Ox)=π ∫^(1)_(0) (6x-6x^4)dx=6π*((x^2/2)-(x^5/5))|^(1)_(0)=
=6π*((1/2)-(1/5))=6π*(3/10)=[b]1,8π[/b]
