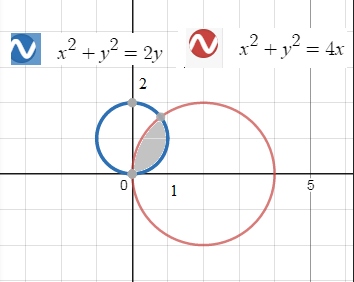
Задача 45350 Найти периметр лунки, образованной...

vk229129367

2020-03-25 18:06:34

Найти периметр лунки, образованной окружностями x^2 + y^2 = 4x и x^2 + y^2 = 2y.

sova

2020-03-25 18:58:58

Надо найти сумму длин дуг окружностей.

Для этого найти точки пересечения окружностей.

Удобнее перейти к полярным координатам:

x= ρ cos θ
y= ρ sin θ

Тогда
x^2+y^2= ρ ^2cos^2 θ + ρ ^2sin^2 θ ⇒

x^2+y^2=p^2

ρ ^2=4* ρ cos θ

ρ =4cos θ - уравнение окружности x^2+y^2=4y

ρ =2sin θ - уравнение окружности x^2+y^2=2y

4cos θ =2sin θ

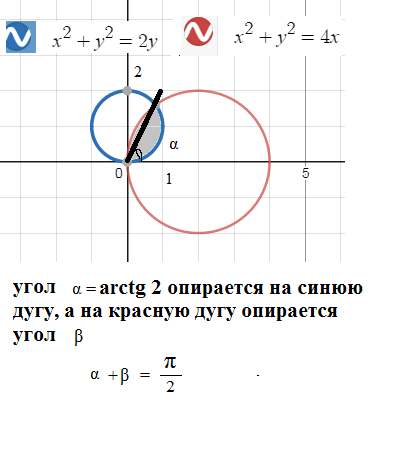
tg θ =2

[b]θ =arctg2[/b]

С=2π*R - формула длины окружности

[r]C=R* α - формула длины дуги в α радиан[/r]

L_(1)- длина дуги синей окружности радиуса 1

L_(1)=arctg2

L_(2)- длина дуги синей окружности радиуса 2

L_(2)=2((π/2)-arctg2)=π-2arctg2

P=L_(1)+L_(2)=arctg2+π-2arctg2=π-arctg2

О т в е т.[b] π-arctg2[/b]