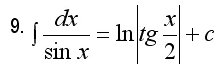Задача 45348 найти длину дуги...
Условие
Решение
[r]L= ∫ ^( β )_( α ) sqrt((r( φ ))^2+(r`( φ ))^2)d φ [/r]
r=(1/ φ )
r`( φ )=-1/ φ ^2
sqrt(r^2+(r`)^2)=sqrt((1/φ)^2+(-1/ φ ^2)^2)d φ=(1/ φ )sqrt( φ ^2+1)
L= ∫ ^( 4/3 )_(3/4 ) (sqrt( φ ^2+1)/ φ )d φ =
[i]замена переменной:[/i]
φ =tgt ⇒ d φ =dt/cos^2t
φ ^2+1=tg^2+1=1/cos^2t
sqrt(φ ^2+1)=1/cost
=∫ ^(arctg( 4/3) )_(arctg(3/4) )(1/cost)/ tgt )d t/cos^2t =
=∫ ^(arctg( 4/3) )_(arctg(3/4) ) dt/(sint*cos^2t)
1=cos^2t+sin^2t
=∫ ^(arctg( 4/3) )_(arctg(3/4) ) (sin^2t+cos^2t)dt/(sint*cos^2t)
=∫ ^(arctg( 4/3) )_(arctg(3/4) ) (sint/cos^2t)dt + ∫ ^(arctg( 4/3) )_(arctg(3/4) ) dt/sint=
=((1/cost)+ln |tg(t/2)|)|^(arctg(4/3)_(arctg(3/4)=
=1/cos(arctg(4/3))-1/cos(arctg(3/4))+ln|tg(arctg(4/3))/2|-ln|tg(arctg(3/4))/2|
Теперь упрощаем
arctg(4/3)= α ⇒ tg α =(4/3) ⇒ cos α =? tg( α /2)=?
cos α =sqrt(1/(1+tg^2 α ))=sqrt(9/25)=3/5 ⇒ sin α =4/5
tg( α /2)=sin α /(1+cos α )=1/2
arctg(3/4)= β ⇒ tg α =(3/4) ⇒ cos α =? tg( α /2)=?
cos α =sqrt(1/(1+tg^2 α ))=sqrt(16/25)=4/5 ⇒ sin α =3/5
tg( α /2)=sin α /(1+cos α )=1/3
О т в е т. =(5/3)-(5/4)+ln(1/2|-ln|1/3|=[b](5/12)+ln(3/2)[/b]
